La collection d'exercices de Vladimir Arnol'd

Par MathOMan, vendredi 25 juin 2010 à 10:24 - Maths pour matheux - Tags - RSS

En 1991 le mathématicien russe Vladimir Arnol'd publia un

Il y vise ceux qu'il appelle les mathématiciens ignorants qui ont étudié les super-variétés ou les théorèmes de plongements mais ne savent pas résoudre des problèmes concrets et simples — ou, avec les mots de Pólya, ceux qui ressemblent à des singes qui sont toujours en haut d'un arbre :

A mathematician who can only generalise is like a monkey who can only climb up a tree, and a mathematician who can only specialise is like a monkey who can only climb down a tree. [...] A real mathematician must be able to generalise and specialise. — George Pólya

Selon Arnold le niveau de la culture mathématique baisse. Et il ne parle pas de la baisse du niveau du bac mais de celle du bac+5. (Or, comme le remarque Martin Andler ici, la question de la baisse de niveau est mal posée à cause de la massification de l'enseignement. Le nombre de mathématiciens en l'an 2000 est beaucoup plus grand que celui en 1900, en absolu et aussi en pourcentage de la population.)
Aux yeux d'Arnold je suis certainement un mathématicien très médiocre, voire ignorant ! De la même manière que je suis étonné quand un étudiant titulaire du bac S puisse avoir du mal à dériver sin(2x) ou à distinguer entre condition nécessaire et condition suffisante, Arnold serait choqué par le fait que je ne sais pas faire d'emblée sa liste de problèmes. En fait, si certains exercices de sa liste me sont très accessibles (par exemple les exercices 45 à 55), il y en a d'autres où je ne sais même pas par où commencer, comme par exemple le no. 72 (un problème de diffusion ?).

Pour Arnold cette collection ne contient pas de questions difficiles, mais seulement des questions qui forment le strict minimum essentiel — il serait alors intéressant de savoir combien un agrégé français moyen en résoudra en une semaine si on lui donne acces à wikipedia et à une bibliothèque de recherche. Quelle est votre estimation ? Plus ou moins que la moitié des problèmes ?

Si on regarde la liste des problèmes proposés on voit bien la préférence de l'auteur pour la géométrie et les équations différentielles. Il y a aussi un peu de topologie algébrique, mais on cherchera en vain des questions d'analyse ou algèbre pures, par exemple.

Vladimir Arnol'd est mort il y a trois semaines pas loin de chez moi, dans l'hôpital Saint-Antoine à Paris.

Mise-à-jour : JLT n'a pas chômé pendant le mois de juillet et a résolu la plupart des exercices !

Restent encore à faire: les no. 27, 41, 51, 58, 68, 69, 70, 73, 74.

Les solutions des exercices se trouvent dans les commentaires (pour déplier cliquer ci-dessous) mais ne sont pas dans l'ordre. Pour s'y retrouver utilisez la fonction find (Ctrl+F) de votre browser et recherchez le numéro de l'exercice par exemple sous la forme "no.54" ou "no.04".

Commentaires

1. Le samedi 26 juin 2010 à 10:49, par MathOMan

Errata de l'énoncé

J'ai trouvé sur le web le trivium d'Arnol'd (en français) en forme de document pdf, je n'en ai pas le fichier tex, donc il m'est impossible de corriger certaines erreurs. Il existe aussi une version en allemand, avec moins de coquilles et une numérotation d'exercices légèrement différente. Voici une liste d'erreurs de la version française :

La date en 2002 donne seulement le jour de compilation de ce fichier français. En fait, Arnol'd a publié sa liste en russe déjà dans l'année 1991 (voir cet entretien).

no.14 — Il manque le dx.

no.27 — Très probablement ça devrait être $\dot z = \epsilon z-(1+i)z|z|^2+\overline z^4.$

no.38 — je suppose que c'est x=..., y=..., z=... et pas x=..., y=..., x=...

no.39 — ... d’un vecteur...

no.37 — ... courbure...
L'énoncé donne une équation qui dépend seulement de deux variables. Il manque certainement une troisième variable pour obtenir une surface (sinon ça serait une courbe dans le plan ou un cylindre dans l'espace, de courbure de Gauss nulle...). Probablement l'équation devrait être
$z^4+(x^2+y^2-1)(2x^2+3y^2-1)=0.$

no.48 — Je crois que ça devrait être z¹⁰.

no.52 — ... forme différentielle...

no.65 — un u superflu ?

no.74 — Le signe de division devrait être la divergence d'un champ de vecteurs.

no.75 — A à la place de Q.

no.78 — Un $\infty$ à la place de infty.

no.79 — Certainement $\varphi(+\infty)=0$ .

2. Le dimanche 27 juin 2010 à 18:48, par JLT

Je pense que l'agrégé moyen ne résoudra pas plus de 40 problèmes en une semaine. Je ne connais pas grand monde qui serait capable de résoudre les 100 problèmes en une semaine, d'ailleurs. Non qu'ils soient réellement difficiles, car je pense que l'ordre de difficulté technique ne dépasse pas, ou pas de beaucoup, celle de l'agrégation à condition d'avoir suivi un cours qui traite du sujet. Peut-être que pour Arnold il était scandaleux que certains de ces sujets ne figurent pas dans le cursus des étudiants, mais je ne suis pas vraiment d'accord avec ce point de vue, chacun a la droit de choisir les matières qu'il préfère. Cela dit, même pour les étudiants qui auraient suivi tous les cours nécessaires, il n'y aurait pas grand monde capable de résoudre tous ces exercices.

Dans mon cas personnel, je n'ai pas la patience de les tester tous (!) mais il y a peut-être une moitié des exercices qui nécessiterait que je me documente, ou alors qui nécessiterait une ou plusieurs heures de réflexion.

P.S. pour la question 72 il faut évidemment utiliser l'équation de la chaleur. Si on note u(x,t) la température en fonction de la profondeur x et du temps t, alors comme u(x,t) est périodique par rapport à t, on peut exprimer la solution en fonction des coefficients de Fourier de u(0,t). La solution est une expression qui fait intervenir $x/\sqrt{T}$ , où T est la période, donc si T est divisée par 365 le sol doit geler jusqu'à une profondeur de $2/\sqrt{365}$ mètre.

Par contre, la plupart des exercices de 45 à 55 nécessiteraient réflexion pour moi...

3. Le dimanche 27 juin 2010 à 19:03, par JLT

Arnold Trivium — Solution du no.72

Bon, j'ai fait des calculs pour rien. Si u(x,t) est solution de l'équation de la chaleur, alors $v(x,t) = u(x/\sqrt{a},t/a)$ aussi, d'où la conclusion indiquée en prenant a=365.

4. Le lundi 28 juin 2010 à 14:06, par MathOMan

Je ne connais pas grand monde qui serait capable de résoudre les 100 problèmes en une semaine, d'ailleurs.

Ah, d'après toutes tes interventions ici et sur d'autres blogs, je pensais justement que tu en faisais partie ;-) Mon ami Fare dit que étais un vrai "crack" lorsqu'il était en sup et toi en spé dans le même lycée.

Concernant ta solution du no.72 je devrais d'abord réviser l'équation de la chaleur (pour comprendre comment interviennent la condition de la température extérieure).

5. Le lundi 28 juin 2010 à 14:12, par MathOMan

Arnold Trivium — Solution du no.54

Par dérivation de w(z) = arctan(z) on trouve

$\forall z\in\mathbb{C}\setminus\{\pm i\}\,,\qquad w'(z)\;=\;\frac1{z^2+1}\;=\;\frac i2\:\left(\frac1{z+i}\;-\;\frac1{z-i}\right).$
Par conséquence la fonction analytique multivaluée w s'obtient en intégrant la fonction univaluée w' le long de tout chemin dans C\{i,- i}. On remarque que le résidu de w' en i (resp. -i) vaut -i/2 (resp. i/2). Notons $\gamma$ (resp. $\mu$ ) un lacet qui contourne le point i (resp. -i) dans le sens direct (resp. indirect).

Soit w₀ un germe analytique de w= arctan(z) en 0 (par exemple celui associé à la fonction réelle arctangente définie sur l'axe réelle). Alors on a pour les prolongements analytiques :

$\begin{align*} \gamma.w_0&=w_0-\frac i2\times2i\pi=w_0+\pi\,, & \mu.w_0&=w_0+\frac i2\times(-2i\pi)=w_0+\pi\,. \end{align*}$

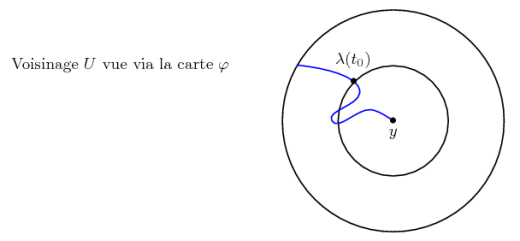
Autrement dit, prolonger un germe de la fonction w par $\gamma$ ou encore par $\mu$ donne le même germe. (Ou encore : le grand tour $\gamma\mu^{-1}$ qui contourne les deux points singuliers est de monodromie nulle.) Ainsi la surface de Riemann de la fonction w= arctan(z) est un revêtement d'ordre infini

$\rho\; :\; {\cal S} \:\longrightarrow\: \mathbb{C}\setminus\{\pm i\}$

dont les propriétés topologiques sont résumées dans le dessin suivant.

Structure de la surface de Riemann de la fonction arctangente.
Un grand tour autour des deux singularités fait revenir au même feuillet.

Le groupe libre de générateurs $\gamma$ et $\mu$ agit de manière simplement transitive sur le revêtement universel de C\{i,- i}. La surface de Riemann $\cal S$ est l'espace quotient de cette action par la relation $\gamma=\mu$ .

6. Le lundi 28 juin 2010 à 14:20, par MathOMan

Arnold Trivium — Solution du no.45

On rappelle que les homographies

$z\mapsto \frac{az+b}{cz+d}\,,\qquad ad-bc\neq0,$

envoient des cercles ou droites sur des cercles ou droites.

Pour l'homographie f(z)=(1+z)/(1-z) on a f(1)=oo, f(-1)=0 et f(i)=i ; on en déduit que f envoie le cercle unité sur l'axe imaginaire. Par conséquence f envoie le disque unité sur l'un des demi-plan délimités par l'axe imaginaire, et comme f(0)=1 il s'agit du demi-plan défini par Re(z)>0.
L'application qui à z associe z² induit une représentation conforme g entre le premier quadrant et le demi-plan défini par Im(z)>0.

Notant r la multiplication par i (rotation de 90°), la composée $g^{-1}\circ r\circ f$ est une représentation conforme de l'intérieur du disque unité sur le premier quadrant.

7. Le lundi 28 juin 2010 à 14:26, par MathOMan

Arnold Trivium — Solution du no.55

Soit P un polynôme complexe de degré n et n'ayant que des racines simples. La surface de Riemann de la fonction $w= \sqrt{P(z)}$ , ou encore la courbe algébrique complexe $\cal S$ d'équation w²=P(z), est un revêtement ramifié à deux feuillets du plan complexe, les points de ramification se situant au-dessus des n racines de P. Considérons un lacet dans $\mathbb{C}$ en forme de cercle de rayon assez grand qui contourne toutes les n racines de P. Si n est pair ce lacet se relève en un lacet dans la surface de Riemann, mais si n est impair le relèvement donne un chemin non-fermé car on change de feuillet.

On compactifie $\cal S$ en ajoutant des points à l'infini comme suit :

si n est pair on ajoute deux points au-dessus de l'infini,

si n est impair on ajoute un point de ramification au-dessus de l'infini.

La surface compactifiée $\overline{\cal S}$ est alors un revêtement ramifié à deux feuillets de la sphère de Riemann ayant un nombre pair de points de ramification, à savoir n si n est pair et n+1 si n est impair. Voici le dessin pour n=5 ou n=6. Les lignes ondulées représentent des coupures où on passe d'un feuillet à l'autre.

Le nombre d'anses, aussi appelé le genre g, est donc

$g=\left\lfloor\frac{n-1}2 \right\rfloor\,,$
où $\lfloor \;\rfloor$ désigne la partie entière. — Exemples :

Si n=1 ou n=2 on voit immédiatement que tout lacet est contractile en un point. Ainsi $\overline{\cal S}$ est simplement connexe et donc isomorphe à la sphère de Riemann. Il n'y pas de anse, c'est-à-dire g=0.

Si n=3 ou n=4 alors le groupe fondamental de $\overline{\cal S}$ possède les deux générateurs du dessin suivant. $\overline{\cal S}$ est isomorphe à un tore et g=1.

8. Le mardi 29 juin 2010 à 12:42, par JLT

Arnold n'était pas avare de critiques envers l'enseignement des mathématiques en France. Voir aussi ce passage et en particulier le paragraphe commençant par To the question "what is 2 + 3". Je pense que l'idée qu'Arnold se faisait de ce qu'un étudiant en mathématiques doit connaître est assez différent de ce qu'un étudiant apprend dans le système scolaire français. Ceci, plus surtout le fait qu'Arnold était un mathématicien largement au-dessus du lot, fait qu'en comparaison nous devons avoir l'air d'handicapés mentaux.

Pour l'exercice no.72 : il n'y a aucune subtilité sur la température extérieure, on suppose que la température de la surface du sol est égal à tout instant à la température extérieure, ce qui impose la condition au bord u(0,t) = température extérieure à l'instant t.

Exercice no.05 : il doit y avoir une erreur car ça me semble trop simple.

Exercice no.50 : ça me semble bizarre car j'ai l'impression que l'intégrale ne converge pas.

Exercice no.54 : comme je n'avais pas fait beaucoup d'analyse complexe quand j'étais jeune, j'ai cherché une solution naïve comme suit. On résout tan(w)=z en exp(2iw)=(1+iz)/(1-iz). Comme une homographie est un automorphisme de la sphère de Riemann, cela revient à exp(2iw)=Z avec Z complexe différent de 0 et -1. Or, exp(2iw)=Z avec Z non nul donne le revêtement universel de C* (qui est C), donc la réponse à la question devrait être C privé des points $\pi/2 + n\pi$ (avec n entier relatif). Cela dit, comme je ne suis pas sûr de comprendre la question, je ne suis pas sûr non plus de la réponse...

9. Le mercredi 30 juin 2010 à 10:11, par MathOMan

Exercice no.72 : Mon problème était que je ne comprenais pas bien la question (et l'équation de la chaleur). Parallèle : en méca, quand je considère l'équation d'une oscillation y'' + ay' + by = f(x) je sais que b est une constante du système, a un facteur de frottement et f une fonction qui impose une force extérieure ; évidemment la solution dépend de cette force. Dans le cas de l'équation de la chaleur je pensais qu'il y avait une fonction périodique sur une année qui donne la température de l'air extérieur et qui ensuite influence celle du sol, puis on pose la question que se passe-t-il dans le sol si cette fonction extérieure change de période (sans changer d'amplitude) ?

Exercice no.54 : C'est amusant ! En fait, le raisonnement de JLT, même s'il n'est pas faux, ne répond pas à la question. Il faut savoir que, lorsqu'on demande de décrire la surface de Riemann S d'une fonction w=f(z), on sous-entend toujours qu'on donne le couple (S,p) où p est la projection sur le plan de la variable z (et non sur le plan des valeurs w). Je vais expliquer cela sur quelques exemples.

Cas d'une fonction algébrique : Soit à décrire la surface de Riemann S de la fonction racine carrée w=z^1/2. On peut identifier S à la courbe algébrique complexe formée des couples (z,w) dans C² vérifiant l'équation w²=z. Sur C², et donc par restriction aussi sur S, on a deux projections p₁ et p₂ définies par
p₁(z,w)=z et p₂(z,w)=w.
C'est la première qu'on veut ! Car (S,p₁) est un revêtement ramifié à deux feuillets au-dessus du plan des z et cela correspond bien au fait que la fonction w, racine carrée de z, possède deux déterminations de signes opposées et qu'on passe de l'une à l'autre en suivant un lacet dans le plan des z autour de l'origine.
En revanche, la deuxième projection est un isomorphisme de S sur le plan des w et a peu d'intérêt dans ce contexte. En fait (S,p₂) est la surface de Riemann de la fonction z=w² qui est univaluée, donc il n'y a rien d'excitant...

Dans le cas de w=arctan(z) on peut effectivement commencer comme JLT et réécrire l'équation sous la forme univaluée z=tan(w), puis identifier la surface de Riemann S à la courbe transcendente dans C² définie par cette équation. L'erreur de JLT est de considérer la mauvaise projection : p₂ au lieu de p₁. Il était prévisible qu'il obtient ainsi comme surface de Riemann C privé de $\pi/2+\mathbb{Z}\pi$ car c'est simplement l'ensemble de définition de la fonction (univaluée) tangente !
La projection p₂ nous apprend rien sur les propriétés de prolongement analytique de la fonction (multivaluée) arctangente. Et la seule manière d'y arriver c'est par des considérations comme je les propose dans ma solution.

Dans le cas général on définit la surface de Riemann S d'un germe analytique w comme étant la composante connexe de w dans l'espace total $|{\cal O}|$ du faisceau ${\cal O}$ des fonctions holomorphes.
Intuitivement cela se résume ainsi : S est le "plus petit" espace étale au-dessus de C sur lequel tous les prolongements analytiques de w induisent une fonction univaluée.
Pour faire le lien avec les deux exemples précédents on constate que sur $|{\cal O}|$ il existe deux applications holomorphes canoniques : l'une associe à un germe u en z₀ le point z₀ et l'autre la valeur u(z₀) du germe en ce point. Ces deux applications correspondent précisément aux projections p₁ et p₂ des exemples précédents...

Résumé : (S,p₁) est la surface de Riemann du germe w tandis que (S,p₂) est celle du germe de fonction réciproque w^-1. La question d'Arnold concerne la première (arctangente), la réponse de JLT la seconde (tangente).

10. Le mercredi 30 juin 2010 à 15:10, par JL

Merci Math ô man de prendre du temps pour les mathématiques comme tu le fais.
Je viens de jeter un oeil à cette feuille d´éxercices et, effectivement, tout n´est pas évident. Je ne saurai pas chiffrer le nombre de personnes capables de résoudre tous ces problémes en un temps reccord, mais une chose est sûre, j´essaierai d´ajouter ma pierre à l´édifice!

Merci encore pour tout,

Un lecteur assidu.

11. Le jeudi 1 juillet 2010 à 00:22, par PB

Pas beaucoup d'exercices d'algèbre ou d'arithmétique en effet dans cette liste. J'aurais aimé par exemple : calculer la signature de la (multiplication par 541 modulo 1223) :-)

12. Le jeudi 1 juillet 2010 à 12:59, par Fabien Besnard

Ce qui est le plus cocasse c'est que cette liste est selon Arnold le minimum pour un... étudiant en physique !

13. Le jeudi 1 juillet 2010 à 14:35, par MathOMan

PB : Calculer la signature de la (multiplication par 541 modulo 1223)

Si je te comprends bien, 541 est inversible dans Z/1223Z et tu cherches la signature de la permutation induite sue Z/1223Z par cette multiplication ?

Jl : j'essaierai d'ajouter ma pierre à l'édifice!

Ah oui, ça serait pas mal si un jour chaque problème de la liste a sa solution postée sur ce blog. Allez-y, postez dans les commentaires ! Si ça devient trop, je ferai le ménage en subdivisant en plusieurs pages ;-)

Fabien : le minimum pour un... étudiant en physique !

Oui, tout à fait ! J'ai quand même l'impression que les physiciens connaissent plus de maths qu'inversement ;-)

14. Le jeudi 1 juillet 2010 à 17:06, par MathOMan

Solution du no.52

Les notations de l'énoncé viennent de la mécanique (potentiel U et niveau d'énérgie E). Nous préférons écrire l'équation sous la forme y²=P(x) où

P=2(E-U)=a₀+a₁x+...+a_nxⁿ

avec des a_k complexes et a_n non-nul. Comme E est une valeur régulière de U les n racines du polynôme P sont simples. La surface de Riemann

${\cal S}=\{(x,y)\in\mathbb{C}^2\,|\,y^2=P(x)\}$
n'est pas compacte. Pour la compactifier il suffit d'ajouter des points à l'infini (voir aussi l'exercice no.45) : deux points Q et Q' si n est pair, et un point R si n est impair. Notons $\overline{\cal S}$ la surface ainsi compactifiée. L'application

$\overline{\cal S} \longrightarrow \mathbb{C} P^1, \;\; \begin{cases} (x,y) \longrightarrow x&\\ Q,Q' \longrightarrow \infty&\text{ si $n$ pair}\\ \phantom{Pr}R \longrightarrow \infty&\text{ si $n$ impair} \end{cases}$
est un revêtement ramifié à deux feuillets. Les points de ramification se situent au-dessus des n racines du polynôme P et au-dessus de l'infini si n impair ; dans tous les cas le nombre de points de ramifications est pair.

Passons maintenant à l'étude des points singuliers de la forme différentielle $\omega = \frac{{\rm d}x}y.$

Soit A=(x₀,y₀) un point dans $\cal S$ . Si $P(x_0)\neq0$ alors $y_0\neq0$ et A est un point régulier de $\omega$ . Si P(x₀)=0 alors P'(x₀) est non-nul et y est une carte locale de $\cal S$ en A. Au voisinage de A on a donc x-x₀=f(y)P(y²) avec une fonction holomorphe f telle que f(y) est non-nul. Ainsi, toujours au voisinage de A,
$\omega=\frac{{\rm d}x}y=\frac{f'(y)y^2+2f(y)y}y{\rm d}y=(f'(y)y+2f(y)){\rm d}y.$

On vient de prouver que $\omega$ n'a pas de singularités dans $\cal S$ . Il reste à étudier ce qu'il en est aux points à l'infini.
Si n est pair, alors $\xi=1/x$ est un carte locale au voisinage de Q et au voisinage de Q'. Comme
$y^2=P(x)=\xi^{-n}(a_n+a_{n-1}\xi+\cdots+a_0\xi^n)$
on a dans ces voisinages de Q et Q'
$\frac1y=\frac{\xi^{n/2}}{g(\xi)},$
où g est holomorphe avec $g(0)=\pm\sqrt{a_n}$ (un signe pour Q, l'autre pour Q'). Par conséquence,
$\omega=\frac{{\rm d}x}y=-\frac{\xi^{n/2-2}}{g(\xi)}{\rm d}\xi.$
Cela montre que la forme différentielle $\omega$ est holomorphe aux points à l'infini si $n\geq4$ pair.
Dans le cas n=2 elle y possède des pôles d'ordre 1, de résidus $\pm1/\sqrt{a_2}$ .

si n est impair alors R est un point de ramification d'ordre 2. La fonction $\xi=1/x$ n'est plus une carte locale au voisinage de R, mais la fonction $\zeta$ définie par $\zeta^2=\xi$ l'est. Comme
$\begin{align*} y^2&=\xi^{-n}(a_n+a_{n-1}\xi+\cdots+a_0\xi^n)\\ &=\zeta^{-2n}(a_n+a_{n-1}\zeta^2+\cdots+a_0\zeta^{2n}) \end{align*}$
on a au voisinage de R
$\frac1y=\frac{\zeta^n}{h(\zeta)},$
où h est holomorphe avec h(0) non-nul. Par conséquence,
$\omega=\frac{{\rm d}x}y=\frac{\zeta^n}{h(\zeta)}{\rm d}(\zeta^{-2})=-\frac{2\zeta^{n-3}}{h(\zeta)}{\rm d}\zeta.$
Cela montre que la forme différentielle $\omega$ est holomorphe au point à l'infini si $n\geq3$ impair.
Dans le cas n=1 elle y possède un pôle d'ordre 2. Son résidu est nul. Cette dernière affirmation résulte du fait que le développement en série de $\zeta^{-2}/h(\zeta)$ n'a pas de puissances impaires.

Résumé : La forme différentielle à étudier est holomorphe sur la surface de Riemann compacte $\overline{\cal S}$ si n>2. Pour n=1 elle possède un seul pôle qui est d'ordre 2 et de résidu nul. Pour n=2 elle possède deux pôles qui sont simples et de résidus opposés.

Remarque : Pour n=1 ou 2 la surface $\overline{\cal S}$ est isomomrphe à la sphère de Riemann CP¹. La somme des résidus de toute forme méromorphe sur CP¹ est finie (car CP¹ est compact) et nulle (car CP¹ est simplement connexe). Nos résultats sur les résidus ne font que confirmer cette propriété plus générale.
Pour n=3 ou 4 la surface $\overline{\cal S}$ est une courbe elliptique. On peut montrer que la primitive de $\omega$ induit un isomorphisme entre $\overline{\cal S}$ et un tore, l'isomorphisme inverse étant $(\wp,\wp')$ où $\wp$ est la fonction de Weierstrass.

15. Le jeudi 1 juillet 2010 à 17:06, par MathOMan

Solution du no.48

D'après l'exercice 52 la forme différentielle dx/y est holomorphe sur la surface de Riemann compacte d'équation y²=1+z¹⁰. Le lacet |z|=2 est contractil sur un point à l'infini. Par conséquence l'intégrale cherchée est nulle.

Remarque : Cette démarche fonctionne pour tout polynôme de degré pair et donne un résultat nul si le degré est supérieur à 2. Si le degré est égal à 2 l'intégrale est non-nulle car le résidu à l'infini ne l'est pas ; on obtient ainsi une méthode un peu tordue pour calculer des intégrales comme

$\int_{-i}^i \frac{{\rm d}z}{\sqrt{1+z^2}}\;,\;\;\;\int_{-1}^1 \frac{{\rm d}x}{\sqrt{1-x^2}}\;,\;\ldots$

JE PARS — BONNES VACANCES A TOUS !

16. Le jeudi 1 juillet 2010 à 17:33, par JLT

Mathoman: merci pour ces explications.

Voici quelques solutions dans le désordre:

Solution du no.57

La fonction u=1 est une solution évidente. En cherchant une solution sous la forme $u=1+\sum_{k\ge 1} b_k(x)y^k$ , on tombe sur la famille de solutions $u=1+\lambda y e^{y^2/2x^2}$

Solution du no.49

D'après le théorème des résidus, l'intégrale de la fonction sur le chemin allant de -R a R, puis parcourant le demi-cercle centre en 0, de rayon R, se trouvant sur le demi-plan supérieur, est égal a $2\pi i Res(e^{ikx}/(1+x^2),i)=\pi e^{-k}$ . On démontre facilement que l'intégrale sur le demi-cercle tend vers 0 quand R tend vers l'infini, donc la réponse est $\pi e^{-k}$

Solution du no.63

On se place en coordonnées polaires. Les coefficients de Fourier de la fonction impaire $u(1,\theta)$ sont $b_n=4/(\pi n)$ pour n impair et 0 sinon. Les fonctions $r^n\sin(n\theta)$ sont harmoniques (soit on le vérifie à la main, soit on observe que c'est la partie imaginaire d'une fonction holomorphe), donc on trouve la solution

$\begin{align*}u&=\sum_{n\ge 1}b_nr^n\sin(n\theta)=\frac{4}{\pi} Im \sum_{k\ge 0} \int z^{2k} dz=\frac{2}{\pi} Im \log\frac{1+z}{1-z}\\ &= \frac{2}{\pi}\mbox{arg}\frac{1+z}{1-z} = \frac{2}{\pi}\arctan\frac{2y}{1-x^2-y^2}\end{align*}$

Solution du no.71

Intuitivement on se dit que la température d'équilibre doit être $u(x,t)=x$ , donc on cherche une solution telle que $u(x,t)=x+v(x,t)$ avec $v(x,t)=x^2-x$ pour t=0 ou bien x=0 ou bien x=1. On peut même prolonger v en une fonction impaire et 2-périodique par rapport à x. On calcule que les coefficients de Fourier de v(x,0) valent $b_n=-8/(n\pi)^3$ pour n impair et 0 sinon. Une méthode de séparation des variables montre que $\sin(n\pi x)e^{\sqrt{n\pi}t}$ est solution de l'équation de la chaleur, donc

$u(x,t)=x+\sum_n b_n \sin(n\pi x)e^{-\sqrt{n\pi}t}$

est solution du problème. Donc $x-(8/\pi^3)e^{-\sqrt{\pi}}\sin\pi x$ est une bonne approximation u(x,1), et on peut en tracer le graphe à la main ou grâce à son logiciel favori.

17. Le jeudi 1 juillet 2010 à 18:07, par JLT

Solution du no.56

en passant en polaires, on voit que $\partial u/\partial\theta =0$ donc l'équation signifie que u ne dépend que de r, d'où l'existence et l'unicité locales de la solution dans le cas où $y_0$ est non nul : $u(r)=\cos\sqrt{r^2-1}$ . Si $y_0=0$ alors il y a une infinité de solutions. En effet, on remarque que $\cos\sqrt{r^2-1}$ a pour dérivée -1 en r=1, donc la restriction de $r\mapsto u(r)$ à $[0,1]$ peut être choisie arbitrairement parmi les fonctions dérivables telles que u(1)=1 et u'(1)=-1.

Solution du no.22

On cherche une solution de la forme y=zx^2. On a

$z'\frac{z}{1+z-2z^2}=\frac{1}{x}$
$\frac{dz}{3}(\frac{1}{1-z}-\frac{1}{1+2z}) =\frac{dx}{x}$
$(1-z)^2(1+2z)=Cx^{-6}$
(j'espere ne pas avoir fait d'erreur de calculs!)

Solution du no.96

Le joueur 1 choisit la piece de 10 centimes avec la probabilite p, et le joueur 2 choisit la piece de 10 centimes avec la probabilite q. L'esperance de gain pour le joueur 2 est

E=10 pq+20(1-p)(1-q)-15p(1-q)-15q(1-p)=60pq+20-35p-35q.

Si p > 35/60, le 2e joueur doit choisir q le plus grand possible.
Si p < 35/60, le 2e joueur doit choisir q le plus petit possible.
Si q < 35/60, le 1e joueur doit choisir p le plus grand possible.
Si q > 35/60, le 1e joueur doit choisir p le plus petit possible.

La strategie optimale est donc p=q=35/60. L'esperance de gain est E=-5/12 donc le jeu n'est pas equitable.

Solution du no.53

Il y a encore des fautes de frappe sur la solution du 53. Voici la version rectifiée.

Le potentiel est $V=\frac{-3}{2}x^2+\frac{x^4}{4}+x$ . Les puits de potentiel sont les minima de V. Notons $x_1<x_2<x_3$ les racines de V'. On constate que V'(-2),...,V'(2) valent respectivement -1,3,1,-1,3 donc
$-2<x_1<-1<0<x_2<1<x_3<2$ . Les puits de potentiel sont en $x_1$ et $x_3$ .

Lorsque x est un minimum local de V, on a V'(x)=0 donc $x^4=3x^2-x$ , ce qui donne $V(x)=\frac{-3}{2}x^2+\frac{3}{4}x^2-\frac{x}{4}+x=\frac{3}{4}(-x^2+x)$ . Comme $-x_1^2+x_1<-2<-x_3^2+x_3$ , on en déduit que le puits le plus profond est en $x_1$ .

Comme $x_1+x_2+x_3=0$ et $x_2>0$ , on voit que $|x_3|<|x_1|$ . Or, $V''(x)=3(x^2-1)$ donc $V''(x_3)<V''(x_1)$ . La période des petites oscillations étant $2\pi/\sqrt{V''(x)}$ , elle est la plus grande dans le puits le moins profond.

Solution du no.39

Notons $\theta$ la longitude et $\varphi$ la latitude. Par simplicité, on redéfinit la longitude de sorte que celle-ci soit égale à 0 à St Petersbourg, et on suppose que la Terre est une sphère de rayon 1. On note $\vec{r}$ le vecteur radial, $\vec{v}$ le vecteur tangent à la Terre dirigé vers le pôle Nord et $\vec{u}$ le vecteur tel que $(\vec{u},\vec{v}\vec{r})$ soit un trièdre orthonormé direct. Soit enfin $\vec{z}$ le vecteur unitaire allant du centre de la Terre vers le pôle Nord.

On paramètre la trajectoire $M_\theta$ au moyen de $\theta$ . On a $\dot{M}_\theta=\vec{z}\wedge M_\theta$ .

Comme $\vec{z}=\sin\varphi \vec{r}+\cos\varphi \vec{v}$ , on a $\dot{u}=\vec{z}\wedge\vec{u}=\sin\varphi\vec{v}-\cos\varphi\vec{r}$ . De même, $\dot{v}=-\sin\varphi\vec{u}$ .

Notons $\frac{D\vec{u}}{\partial \theta}$ la dérivée covariante de $\vec{u}$ le long de la trajectoire. Si P désigne la projection orthogonale sur l'espace tangent à la Terre, on a
$\frac{D\vec{u}}{\partial \theta}=P\dot{u}=\sin\varphi \vec{v}$ . On obtient de même $\frac{D\vec{v}}{\partial \theta}=P\dot{v}=-\sin\varphi \vec{u}$ .

Le vecteur tangent $a(\theta)\vec{u}+b(\theta)\vec{v}$ est donc parallèle si $\dot{a}=-(\sin\varphi)b$ et $\dot{b}=(\sin\varphi)a$ . Ceci s'intègre en
$a(\theta)=-\sin(\theta\sin\varphi)$ et $b(\theta)=\cos(\theta\sin\varphi)$ (compte tenu de la condition initiale a(0)=0 et b(0)=1 qui indique que le vecteur pointe vers le Nord).

On voit que en $\theta$ , le transporté le long d'un parallèle fermé du vecteur unitaire pointant vers le Nord est égal au vecteur obtenu par une rotation d'angle $2\pi\sin\varphi=\pi\sqrt{3}$ du vecteur unitaire pointant vers le Nord.

Solution du no.60

On considère le système différentiel $\dot{x}=y$ , $\dot{y}=\sin x$ . L'énergie $E=\frac{1}{2}y^2+\cos x$ est conservée sur les courbes intégrales. On a donc $y=\pm\sqrt{2(E-\cos x)}$ , ce qui permet de dessiner les courbes intégrales. Je ne sais pas comment insérer des images sur ce blog, mais par tout point de l'axe des ordonnées passe une et une seule courbe intégrale qui ressemble vaguement à une sinusoïde. De plus, il y a des courbes fermées autour de $\pi$ ne coupant pas l'axe des y. Enfin, la figure est invariante par translation de $(2\pi,0)$ , et symétrique par rapport aux deux axes de coordonnées.

En x=0, on a $y^2=2(E-1)$ donc $u(0,y)=4(E-1)^2$ . En remplaçant E par $\frac{1}{2}y^2+\cos x$ , on obtient une solution
$u(x,y)=4(\frac{1}{2}y^2+\cos x-1)^2$ .

La solution n'est pas unique car on peut modifier u arbitrairement sur les courbes intégrales fermées à condition que u soit constante sur celles-ci.

18. Le jeudi 1 juillet 2010 à 18:59, par JLT

Solution du no.64

Infinie. Exemples de solutions: $(r^n+r^{-n})\cos n\theta$ .

Solution du no.65

On regarde les fonctions u=f(r) ne dependant que de r.
On cherche donc a minimiser $\int_0^1 f'(r)^2 rdr$ .
Considerons $f(r)=\mbox{max}(0,1-\log(r)/\log(\varepsilon)$ .
Alors $\int_0^1 f'(r)^2 rdr =1/\log\varepsilon$ est aussi petit qu'on veut. La fonction f n'est pas $C^\infty$ mais on peut l'approximer par des fonctions $C^\infty$ , donc l'inf cherche est 0.

Solution du no.91

Si u est un endomorphisme d'un espace vectoriel reel E verifiant $u^5=Id$ alors le theoreme des noyaux assure que E est la somme directe des sous-espaces stables

$\mbox{ker}(u-Id)$
$\mbox{ker}(u^2-2\cos(2\pi/5)u+Id)$
$\mbox{ker}(u^2-2\cos(4\pi/5)u+Id)$

Dans le cas qui nous concerne, le premier espace est engendre par le vecteur (1,1,1,1,1),

Le deuxieme espace est engendre par les parties reelles et imaginaires de
$(1,\omega,...,\omega^4)$ ou $\omega=e^{2\pi i/5}$ .

Le troisieme espace est engendre par les parties reelles et imaginaires de
$(1,\zeta,...,\zeta^4)$ ou $\zeta=e^{4\pi i/5}$ .

19. Le vendredi 2 juillet 2010 à 09:09, par JLT

Solution du no.59

On considère le système différentiel $\dot{x}=y$ , $\dot{y}=-\sin x$ . Il s'agit de l'équation du pendule (dans l'espace des phases). L'énergie $E=\frac{1}{2}y^2-\cos x$ est conservée (pour le vérifier, il suffit de dériver E par rapport à t). Les courbes intégrales près de l'origine sont des courbes fermées qui ressemblent à des cercles. Le long d'une courbe, on a
$\frac{du}{dt}=\dot{x}\frac{\partial u}{\partial x}+\dot{y}\frac{\partial u}{\partial y}=u^2\ge 0$ .

Comme les courbes intégrales près de l'origine sont fermées, on doit avoir $u=0$ sur celles-ci, donc u=0 dans un voisinage de l'origine.

Solution du no.46

Soit $f(z)=z+c/z$ , avec 0<c<1. Elle est injective sur l'extérieur du disque unité. En effet, l'équation $Z=f(z)$ équivaut à $z^2-zZ+c=0$ , donc le produit des racines est c. L'une d'entre elles doit donc être de module <1.

Pour $z=e^{i\theta}$ , on a $f(z)=(1+c)\cos\theta + i(1-c)\sin\theta$ , donc on peut envoyer l'extérieur du disque unité sur l'extérieur d'une ellipse d'excentricité arbitraire. En composant avec une similitude directe, on se ramène à une ellipse quelconque.

Solution du no.47

Pour se fixer les idées, on suppose que le demi-plan est $y>1$ et que le segment est $[i,2i]$ . L'homographie $z\mapsto 1/z$ envoie cette figure sur le cercle de centre $-i/2$ et de rayon 1/2 privé d'un rayon. On se ramène par une similitude au cercle de centre 0 et de rayon 1 privé du rayon [0,1]. L'application $z\mapsto z+1/z$ l'envoie sur le plan privé de $[-2,+\infty[$ . En composant avec $z\mapsto -(z+2)$ on se ramène au plan privé des réels négatifs. Puis, en composant avec la racine carrée on obtient le demi-plan $x>0$ .

Solution du no.10

Il revient au meme de chercher le comportement asymptotique de z=-y^2. Comme $x^5-x^2z=-z^3$ , on a $z(x-z)(x+z)=x^5$
donc l'un des z, x-z ou x+z doit etre petit par rapport a x.

1er cas: z est petit par rapport a x. Alors z est equivalent a x^3. Comme
$z=\frac{x^3}{1-zx^{-2}} = x^3(1+(zx^{-2})+(zx^{-2})^2+...)$ , on peut determiner de proche en proche le developpement asymptotique de z. Par exemple, $z=x^3+x^7 +o(x^7)$ .

2e cas: x-z est petit par rapport a x. Alors x-z est equivalent a $x^3/2$ . Posons u=x-z. Alors $(x-u)u(2x+u)=x^5$ donc
$u=(x^3/2)(1-\frac{u}{x})^{-1}(1+\frac{u}{2x})^{-1}$ donc on peut ecore determiner le developpement asymptotique de proche en proche.

Le 3e cas est analogue, j'ai la flemme de l'ecrire.

Fini pour aujourd'hui...

20. Le samedi 3 juillet 2010 à 09:40, par JLT

Solution du no.92

Notons $E_n$ l'espace des polynômes réels homogènes à trois variables de degré n. Comme il est engendré par les monômes $x^ay^bz^c$ avec $a+b+c=n$ , il est de dimension 1+2+...+(n+1) = (n+1)(n+2)/2.

Il s'identifie au sous-espace de $E_1^{\otimes n}$ qui consiste en les tenseurs symétriques, donc possède un produit scalaire invariant sous l'action de SO(3). Concrètement, les monômes $x^ay^bz^c$ sont de norme $\sqrt{\frac{a!b!c!}{n!}}$ et sont deux à deux orthogonaux.

Notons $P=x^2+y^2+z^2$ . Ce polynôme est invariant sous l'action de SO(3), donc les sous-espaces $P^2 E_1$ et $PE_3$ de $E_5$ sont stables. On a donc une décomposition

$E_5= F_1 \oplus F_2 \oplus F_3$ ,

où les $F_i$ sont respectivement $P^2E_1$ , l'orthogonal de $F_1$ dans $PE_3$ et l'orthogonal de $PE_3$ dans $E_5$ . On a ainsi exhibé une décomposition en somme directe de trois sous-espaces de dimensions 3, 7 et 11 respectivement. Il reste à montrer que ces derniers sont irréductibles. Il suffit pour cela de voir que leurs complexifiés le sont. Comme SO(3) est un quotient de SU(2), il est équivalent de montrer que le complexifié de $S^5(E_1)$ est somme directe de trois sous-espaces irréductibles sous l'action de SU(2).

Rappelons les faits suivants sur la théorie des représentations de SU(2) (que je connais moins mal que SO(3) !)

1) Soient $\sigma_1$ la représentation triviale, $\sigma_2$ la représentation tautologique et $\sigma_n$ la $(n-1)$ -ième puissance symétrique de $\sigma_2$ . C'est une représentation irréductible de dimension n, et toute représentation irréductible de SU(2) est équivalente à une et une seule des $\sigma_n$ .

2) Si $\pi$ est une représentation de dimension finie de SU(2), on note $\chi_\pi(z)=\mbox{Tr}\pi(\mbox{diag}(z,z^{-1}))$ (z complexe de module 1) le caractère de $\pi$ . C'est un polynôme à coefficients entiers en $z+z^{-1}$ .

3) Soit $T_n$ le polynôme de Tchebycheff de 2e espèce défini par $T_n(z+z^{-1})=z^{-n}+z^{-n+2}+z^{-n+4}+\cdots+z^n$ . Autrement dit, $T_n(2\cos\theta)=\frac{\sin (n+1)\theta}{\sin\theta}$ . Alors le caractère de $\sigma_n$ est $T_{n-1}(z+z^{-1})$ .

4) Si une représentation a pour caractère $\sum_{i=1}^N z^{m_i}$ (avec répétition possible des $m_i$ ), alors sa k-ième puissance symétrique a pour caractère $\sum z^{a_1m_1+\cdots+a_Nm_N}$ , où les $(a_i)$ parcourent les N-uplets d'entiers positifs ou nuls vérifiant $a_1+\cdots+a_N=k$ .

Considérons le complexifié de $E_1$ . Comme il est de dimension 3 et n'a pas de vecteur invariant, il est nécessairement irréductible, donc isomorphe à $\sigma_3$ dont le caractère est $z^{-2}+1+z^2$ . Sa 5e puissance symétrique a pour caractère

$\begin{array}{rcl} \sum_{a+b\le 5}z^{2(a-b)}&=&3+3(z^2+z^{-2})+2(z^4+z^{-4})+2(z^6+z^{-6})\\ &&\;+(z^8+z^{-8})+(z^{10}+z^{-10}).\end{array}$

Le complexifié de $S^5E_1$ a donc pour caractère $(T_2+T_6+T_{10})(z+z^{-1})$ , qui est le même que celui de $\sigma_3\oplus \sigma_7\oplus\sigma_{11}$ donc ces représentations sont équivalentes. CQFD.

Solution du no.93

Notons n=3600. Pour calculer la probabilité de recevoir exactement k appels dans une seconde donnée, on doit d'abord sélectionner k abonnés parmi n. Ceux-ci ont chacun une probabilité 1/n de téléphoner dans cette seconde, tandis que les n-k autres ont chacun une probabilité 1-1/n de ne pas téléphoner dans cette seconde. La probabilité de recevoir exactement k appels est donc

$\frac{C_n^k}{n^k}(1-1/n)^{n-k}$ qui vaut approximativement 1/(k!e). La probabilité de recevoir 5 appels ou plus dans une seconde donnée est donc $p=1-\sum_{k=0}^4 \frac{C_n^k}{n^k}(1-1/n)^{n-k} \simeq 1-65/(24e)\simeq 0,0037$ .

Le temps moyen entre deux telles secondes est p+2p(1-p)+3p(1-p)^2+... = 1/p, qui vaut environ 273 secondes.

21. Le dimanche 4 juillet 2010 à 09:36, par JLT

Arnold Trivium — Solution du no.12

On vérifie que la divergence du champ de vecteurs est nulle. D'après le théorème de Green-Ostrogradski, son flux à travers n'importe quelle surface fermée est nul.

22. Le dimanche 4 juillet 2010 à 17:49, par JLT

Solution du no.62
Solution du no. 62

Première question :

On traite d'abord le cas où b=0. En paramétrant le cercle par $x=a+R\cos\theta, y=R\sin\theta$ , on voit que la moyenne de log(r) sur le cercle est l'intégrale
$I=\frac{1}{4\pi}\int_0^{2\pi} \log(a^2+R^2+2aR\cos\theta)\,d\theta$

Notons $I(x)=\frac{1}{2\pi}\int_0^{2\pi} \log(1+x^2+2x\cos\theta)\,d\theta$ , pour $|x| < 1$ .

Lorsque $z=e^{i\theta}$ , on a $d\theta=\frac{dz}{i z}$ , donc
$I(x)=\frac{1}{2\pi i}\oint_\gamma \log((1+xz)(1+xz^{-1}))\,\frac{dz}{z}$ ,
où $\gamma$ désigne le cercle unité orienté dans le sens trigonométrique.

L'intégrale $\frac{1}{2\pi i}\oint_\gamma \log(1+xz)\,\frac{dz}{z}$
est nulle d'après le théorème des résidus.

L'intégrale $\frac{1}{2\pi i}\oint_\gamma \log(1+xz^{-1})\,\frac{dz}{z}$
est également nulle, en effectuant le changement de variables u=1/z et en appliquant le théorème des résidus.

On a donc I(x)=0 si $|x| < 1$ .

Montrons que l'on a toujours I(x)=0 pour x=1 ou x=-1. Montrons-le par exemple pour x=-1. Il suffit de voir que I(x) est continu lorsque x tend vers -1 par valeurs supérieures; ceci est une conséquence facile du théorème de convergence dominée et de l'inégalité $1+x^2+2x\cos\theta\ge \sin^2\theta$ .

Si $a\le R$ , comme $\log(a^2+R^2+2aR\cos\theta)=2\log R +\log(1+(a/R)^2+2(a/R)\cos\theta)$ on a $I=\log R$

Si a>R, on montre de même $I=\log a$ .

On en conclut donc que, dans le cas général, $I=\log \mbox{max}(R,\sqrt{a^2+b^2})$ .

Deuxième question :

Notons R le rayon de la sphère et a la distance entre la sphère et l'origine. Après changement d'origine, on peut supposer que l'origine est au centre de la sphère, et que l'origine initiale a pour coordonnées (0,0,a). On se place en coordonnées polaires par rapport au centre de la sphère. Celle-ci est donc paramétrée par
$x=R\cos\theta\cos\varphi, y=R\sin\theta\cos\varphi, z=R\sin\varphi$ .
L'élément de surface est $dS=R^2\cos\varphi\,d\theta d\varphi$ . On doit donc calculer

$I=\frac{1}{4\pi}\int\int_{[0,2\pi]\times [-\pi/2,\pi/2]} \frac{\cos\varphi\,d\theta d\varphi}{\sqrt{R^2\cos^2\varphi+(R\sin\varphi-a)^2}}\,d\theta d\varphi$
$= \frac{1}{2}\int_{-\pi/2}^{\pi/2}\frac{\cos\varphi\,d\varphi}{\sqrt{R^2+a^2-2aR\sin\varphi}}\,d\varphi$
$= \frac{1}{2}\int_{-1}^{1}\frac{dt}{\sqrt{R^2+a^2-2aRt}}$
$= \frac{1}{2aR} (|a+R|-|a-R|) = \frac{1}{\mbox{max}(a,R)}$ .

Remarque : du point de vue physique, cela signifie que le potentiel gravitationnel créé par une coquille sphérique homogène de masse m est le même, à l'extérieur de la coquille, que celui créé par une masse m placée au centre de la sphère, ce qui justifie qu'en mécanique céleste on assimile les planètes à des points matériels. Par contre, à l'intérieur de la coquille, le potentiel gravitationnel est constant, ce qui indique qu'un objet placé à l'intérieur serait en apesanteur.

23. Le dimanche 4 juillet 2010 à 18:08, par JLT

Arnold Trivium — Solution du no.18
On doit intégrer exp(-q(x)), où q est une forme quadratique dont la matrice A a des 1 sur la diagonale et 1/2 ailleurs. On a donc A=(I+E)/2, où I est la matrice identité et E est la matrice avec des 1 partout. Comme E est de rang 1, autoadjoint et vérifie $E^2=nE$ , E est égal à nP, où P est un projecteur orthogonal de rang 1. On en déduit que A=(I+nP)/2 a pour valeurs propres (n+1)/2 (de multiplicité 1) et 1/2 (de multiplicité n-1).

En effectuant un changement orthogonal de coordonnées, on se ramène à intégrer exp(-q(x)) où
$q(x)=(n+1)x_1^2/2+x_2^2/2+\cdots +x_n^2/2$ .

Or, il est connu que $\int_{-\infty}^\infty e^{-ax^2}\,dx=\sqrt{\pi/a}$ , donc l'intégrale à calculer vaut
$\pi^{n/2}\sqrt{2^n/(n+1)}$ .

24. Le dimanche 4 juillet 2010 à 18:15, par JLT

Solution du no.81
La première forme quadratique est positive et son noyau est visiblement la droite engendrée par (1,1,...,1), donc elle est de rang n-1. Par conséquent, il y a n-1 carrés positifs et aucun carré négatif.

Pour la deuxième forme quadratique, sa matrice est (nP-I)/2 où on a utilisé les notations de l'exercice 18. Si n>1, il y a donc 1 carré positif et n-1 carrés négatifs. Si n=1 la forme est nulle.

Solution du no.82
Il doit y avoir une erreur d'énoncé car ce n'est pas un ellipsoïde mais un hyperboloïde. Je pense qu'il faut remplacer l'inégalité stricte par une inégalité large. Dans ce cas, d'après la solution de l'exercice 18, il y a n-1 axes de longueur $2\sqrt{2}$ et un axe de longueur $\sqrt{8/(n+1)}$ .

25. Le dimanche 4 juillet 2010 à 18:48, par JLT

Solution (?) du no.19
Ici je ne suis pas sur de ce que doit être la solution complète au problème. On a dx/ds = const/n(y) et $(ds)^2=(dx)^2+(dy)^2$ donc
$const. n(y)^2=1+(dy/dx)^2$ , ce qui donne
$\frac{dy}{sqrt{Cn(y)^2-1}}=dx$

mais je ne vois pas de moyen d'intégrer cette fonction.

26. Le lundi 5 juillet 2010 à 09:48, par JLT

Solution du no.61
Pour la première question, supposons qu'une telle fonction u existe. On peut supposer que la restriction de $\nabla u$ à la parabole est le vecteur normal unitaire rentrant.

Fixons un point M de la parabole. Considérons la solution $f(t)$ du problème de Cauchy f(0)=M, $f'(t)=(\nabla u)(f(t))$ .

Pour $t\ge 0$ , on a d/dt(u(f(t)))=1, donc u(f(t))=t+1. De plus, comme u et f sont 1-Lipschitziennes, $t=u(f(t))-u(f(0))\le ||f(t)-f(0)||\le t$ , donc on voit que l'image de f est une géodésique. Autrement dit, si $\vec{n}$ est le vecteur normal en M, on a $f(t)=M+t\vec{n}=M+(u(f(t))-1)\vec{n}$ . Si maintenant deux normales en M et M' à la parabole se coupent en un point A, on en déduit que AM=u(A)-1=AM'. Or, il est facile de trouver deux points sur la parabole (par exemple M=(0,0) et M'=(10,100)) tels que l'égalité précédente ne soit pas satisfaite. Contradiction.

Pour la deuxième question, montrons que la fonction u(A)=(1+distance entre A et la parabole) convient. Paramétrons la parabole par $M(x)=(x,x^2)$ . Soit $\vec{n}(x)$ le vecteur normal en M(x), unitaire, dirigé vers l'extérieur. On a $u(M(x)+t \vec{n}(x))=t+1$ , donc si u est différentiable, son gradient est de norme au moins 1. De plus, comme u est 1-Lipschitzienne, son gradient est de norme au plus 1, donc de norme 1.

Il reste à prouver que u est différentiable. Soit $h(x,t)=M(x)+t \vec{n}(x)$ . On vérifie que la différentielle de h est inversible en tout point $(x,t)\in \mathbb{R}\times \mathbb{R}_+^*$ . De plus, h est une bijection entre $\mathbb{R}\times \mathbb{R}_+^*$ et le dessous de la parabole. D'après le théorème d'inversion globale, h est un difféomorphisme. Comme u(h(x,t))=t+1, on en conclut que u est bien différentiable donc est une solution du problème de Cauchy.

27. Le lundi 5 juillet 2010 à 10:41, par JLT

Solution du no.86
Zéro. Ceci peut se vérifier directement en utilisant la formule du double produit vectoriel, ou bien en identifiant $\mathbb{R}^3$ muni du produit vectoriel à l'algèbre de Lie de SO(3).

Solution du no.87
Zéro.

Solution du no.88
On identifie l'espace des quasi-polynômes de l'énoncé avec l'espace E des polynômes de degré au plus 5 au moyen de l'isomorphisme $p(t)\mapsto e^{\lambda t}p(t)$ . L'opérateur de dérivation sur les quasi-polynômes s'identifie à $\lambda Id + D$ où D est la dérivation des polynômes. L'exponentielle de cet opérateur est $e^\lambda \mbox{exp}(D)$ . Or, D est nilpotent et son noyau est de dimension 1, donc $e^D-I=D(I+D/2+D^2/3!+...)$ aussi. $e^D$ a donc pour forme de Jordan la matrice avec des 1 sur la diagonale et des 1 juste au-dessus, donc l'opérateur de l'énoncé a pour forme de Jordan la matrice avec des $e^\lambda$ sur la diagonale et des 1 juste au-dessus.

Pour la 2e question, si $a_i$ sont les valeurs propres de A, alors sur la base de l'espace des matrices carrées d'ordre n constituée par les matrices élémentaires, l'opérateur $\mbox{ad}_A$ est diagonal de valeurs propres $a_i-a_j$ .

28. Le mardi 6 juillet 2010 à 08:32, par JLT

Solution du no.09
Non. L'idée est de considérer les polynômes de la forme $a(y)x^2+2b(y)x+c(y)$ . Pour y fixé, le minimum est $(ac-b^2)/a$ , donc il suffit de prendre $c=1, b=y, a=y^2+1$ .
Le polynôme $P(x,y)=(1+xy)^2+x^2$ est donc un contre-exemple, ce qui peut aussi se vérifier directement car P est strictement positif et vérifie $P(x,-1/x)=x^2$ .

29. Le mardi 6 juillet 2010 à 19:27, par JLT

Arnold Trivium — Solution du no.11
Elle est divergente. En effectuant le changement de variables u=xy, on voit que l'intégrale vaut

$4\int_{\mathbb{R}_+^2}\frac{dudx}{(1+u^4)x} = +\infty$

30. Le mardi 6 juillet 2010 à 19:30, par JLT

Précision sur le no. 51: ceci n'est valable que pour $k\ge 0$ . Si $k\le 0$ , on se ramène à ce qui précède en effectuant le changement de variables $y=-x$ . Pour tout k réel, l'intégrale vaut donc $\pi e^{-|k|}$ .

31. Le mardi 6 juillet 2010 à 20:23, par JLT

Solution du no.78
Soit D l'opérateur différentiel $d^2/dx^2-1$ .
On cherche une fonction g(x) telle que $D(g)=\delta_0$ , donc tel que $D(g\ast u)=u$ . On peut trouver g en utilisant la transformée de Fourier et l'exercice 49 (en effet, en Fourier l'opérateur D s'identifie à la multiplication par $-(1+\xi^2)$ ; d'ailleurs ceci permet de voir que D est injectif). On trouve $g(x)=-\frac{1}{2}e^{-|x|}$ . On peut aussi vérifier directement que cette fonction convient.

Pour la deuxième question, on cherche u tel que $-2g\ast u=e^{-x^2}$ , donc $-2u = D(-2g\ast u)=D(e^{-x^2})=(-2+4x^2)e^{-x^2}$ .
On en déduit que $u(x)=(1-2x^2)e^{-x^2}$ . Réciproquement, si $u(x)=(1-2x^2)e^{-x^2}$ alors $D(-2g\ast u)=D(e^{-x^2})$ , donc comme D est injective, $-2g\ast u=e^{-x^2}$

32. Le mardi 6 juillet 2010 à 20:36, par JLT

Solution du no.66
L'angle solide selon lequel le point A voit une surface S dont le contour est C est l'intégrale

$\int_{M\in S} \frac{\vec{AM}\cdot\vec{n}\,dS}{AM^3}$ ,

où $\vec{n}$ est un vecteur normal unitaire. Cet angle solide ne dépend que de C (et non de S), d'après la solution de l'exercice 12.

Pour vérifier que c'est une fonction harmonique, d'après les théorèmes de dérivation sous l'intégrale, de vérifier que pour tout vecteur $\vec{n}$ et tout point M, la fonction $A\mapsto \frac{\vec{AM}\cdot\vec{n}}{AM^3}$ est harmonique. En appliquant une rotation et une translation, on se ramène au cas où M=O et $\vec{u}=(0,0,1)$ , donc à vérifier que $(x,y,z)\mapsto \frac{z}{(x^2+y^2+z^2)^{3/2}}$ est harmonique. C'est un calcul (presque) immédiat.

33. Le mercredi 7 juillet 2010 à 20:03, par JLT

Solution du no.89
Soit G le groupe des rotations du cube. Il comprend :

- l'identité
- 6 retournements d'axes passant par le milieu d'une arête
- 8 rotations d'axe passant par un sommet et d'angle $2\pi/3$
- 3 retournements d'axes passant par les centres des faces
- 6 rotations de vecteur passant par le centre d'une face et d'angle $\pi/2$ .

G est donc d'ordre au moins 24. Or, le stabilisateur d'un sommet A consiste en les rotations de vecteur $\vec{OA}$ et d'angle $2k\pi/3$ ( $k=0,1,2$ ), donc $24\le |G|=3|\mbox{orb}(A)|\le 24$ . On en déduit que G consiste bien en la liste des 24 rotations énumérées ci-dessus, et qu'il agit transitivement sur les sommets du cube.

L'action de G sur le cube induit une action sur l'ensemble des grandes diagonales, donc un morphisme $G\to S_4$ . Or, si une application linéaire de $\mathbb{R}^3$ dans lui-même laisse stable quatre droites telles que trois d'entre elles ne soient pas coplanaires, alors c'est une homothétie (ceci est un petit exercice d'algèbre linéaire). Comme G ne contient pas d'homothétie autre que l'identité, G agit fidèlement sur l'ensemble des grandes diagonales, donc le morphisme $G\to S_4$ est injectif. Comme G et $S_4$ ont le même cardinal, $G\to S_4$ est un isomorphisme.

Via l'identification entre G et $S_4$ , les rotations énumérées ci-dessus correspondent respectivement à:
- l'identité
- les transpositions
- les 3-cycles
- les doubles-transpositions
- les 4-cycles.

Les sous-groupes de $S_4$ ont un ordre divisant 24, donc ont un ordre parmi 1, 2, 3, 4, 6, 8, 12, 24.

Sous-groupe d'ordre 1 : $\{\mbox{Id}\}$ .

Les sous-groupes d'ordre 2 sont engendrés par un élément d'ordre 2, c'est-à-dire par une transposition ou une double transposition.

Les sous-groupes d'ordre 3 sont engendrés par un 3-cycle.

Les sous-groupes d'ordre 4 qui sont cycliques sont engendrés par un 4-cycle.

Le sous-groupe constitué de l'identité et des 3 doubles-transpositions est distingué, et isomorphe au groupe de Klein $V_4$ .

Les sous-groupes d'ordre 4 engendrés par deux transpositions qui commutent sont de la forme $\{\mbox{Id},(ab),(cd),(ab)(cd)\}$ et sont isomorphes au groupe de Klein. Ils coïncident avec les sous-groupes engendrés par une transposition et une double-transposition qui commutent.

On voit facilement qu'il n'y a pas d'autres sous-groupes d'ordre 4.

Les sous-groupes d'ordre 6 ne peuvent pas être abéliens, sinon G contiendrait un élément d'ordre 6. Ils sont donc isomorphes au groupe symétrique $S_3$ , qui est isomorphe au groupe diédral $D_3$ , donc sont engendrés par deux permutations $\sigma, \tau$ d'ordres 3 et 2 respectivement, vérifiant $\tau\sigma\tau=\sigma^{-1}$ . Par conséquent, $\sigma$ est un 3-cycle $(abc)$ et $\tau$ est une permutation conserve le support de $\sigma$ . On en déduit que $\tau$ est une permutation de $\{a,b,c\}$ . Comme $\tau$ est d'ordre 2, c'est une transposition. On voit donc que les sous-groupes d'ordre 6 sont les $S_{\{a,b,c\}}$ .

Les sous-groupes d'ordre 8 ne peuvent pas comporter uniquement des éléments d'ordre 2, sinon ils devraient être engendrés par trois éléments distincts $\sigma_1,\sigma_2,\sigma_3$ d'ordre 2 qui commutent entre eux, tels que $\sigma_1\sigma_2\sigma_3\ne \mbox{Id}$ . Comme les doubles transpositions engendrent un groupe d'ordre 4, l'un des $\sigma_i$ , par exemple $\sigma_1$ , est une transposition. Comme $\sigma_2,\sigma_3$ commutent à $\sigma_1$ , ils figurent parmi $\{(cd),(ab)(cd)\}$ , ce qui contredit $\sigma_1\sigma_2\sigma_3\ne 1$ .

Les sous-groupes d'ordre 8 ne sont pas non plus cycliques, donc sont isomorphes au groupe diédral $D_4$ ou au groupe quaternionique $H_8$ .

Les sous-groupes isomorphes à $D_4$ sont engendrés par deux permutations $\sigma, \tau$ d'ordres 4 et 2 respectivement, vérifiant $\tau\sigma\tau=\sigma^{-1}$ , donc sont de la forme $\sigma=(abcd)$ et $\tau=(ac)$ .

Si un sous-groupe est isomorphe à $H_8$ , il est engendré par deux éléments $\sigma,\tau$ d'ordre 4 ne commutant pas tels que $\sigma^2=\tau^2$ . On a donc $\sigma=(abcd)$ et $\tau=(axyz)$ avec a,b,c,d distincts, a,x,y,z distincts, y=c. Ceci contredit le fait que $\sigma\tau\ne\tau\sigma$ . Il n'y a donc pas de sous-groupe isomorphe à $H_8$ .

L'unique sous-groupe d'ordre 12 est $A_4$ . En effet, un sous-groupe d'indice 2 est distingué, donc doit être le noyau d'un morphisme non trivial de $S_4$ sur $\{-1,1\}$ . Or, il est bien connu que la signature est l'unique morphisme non trivial de $S_n$ dans $\{-1,1\}$ .

G est l'unique sous-groupe d'ordre 24.

Géométriquement, les sous-groupes isomorphes à $D_4$ sont engendrés par un quart de tour d'axe passant par le centre d'une face et un demi-tour d'axe perpendiculaire au précédent, passant par le milieu d'une arête. On pourra de même expliciter le sous-groupe du groupe des rotations du cube correspondant à chacun des sous-groupes de permutations ci-dessus.

34. Le mercredi 7 juillet 2010 à 22:17, par JLT

Solution du no.90
Notons K l'ensemble des sommets du cube. Soit G le groupe des rotations de K.

On place l'origine au centre du cube. On fixe un repère tel que les sommets du cube sont $(\pm 1,\pm 1,\pm 1)$ . On décompose K en deux tétraèdres réguliers

$X=\{(a,b,c)\in K /\; abc=1\}$
$Y=\{(a,b,c)\in K /\; abc=-1\}$

(Cela revient à colorier un sommet sur deux en noir et un sur deux en blanc.) On vérifie à la main que tout élément de G envoie X sur lui-même ou bien sur Y, et que l'unique sous-groupe d'indice 2 de G est $\{g\in G /\; g\cdot X=X\}$ .

L'espace E des fonctions définies sur les sommets du cube se décompose en somme directe de deux sous-espaces stables sous l'action de G : $E=A\oplus S$ , où A est l'espace des fonctions antisymétriques et S l'espace des fonctions symétriques.

Notons C l'espace des fonctions constantes, et D la droite engendrée par $f_0=1_X-1_Y$ . On vérifie que, si $\chi$ désigne l'unique morphisme de groupes non trivial de G dans $\{-1,1\}$ (qui correspond à la signature via l'identification de G à $S_4$ ), alors
$g\cdot f_0=\chi(g)f_0$ .

Les droites C et D sont donc stables. Notons C' et D' leurs orthogonaux dans S et A respectivement. On a une décomposition de E en somme directe de sous-espaces stables par G :
$E=C\oplus C'\oplus D\oplus D'$
Ces espaces sont de dimensions respectives 1, 3, 1, 3.

Montrons qu'il s'agit bien de la décomposition en sous-espaces irréductibles. Pour cela, il suffit de voir que C' et D' ne contiennent pas de droite stable, donc on se ramène à montrer que les seules droites stables de E sont C et D.

Soit $\Delta$ une droite stable. On fixe un vecteur directeur unitaire $f$ . Comme G agit par isométries sur E, pour tout $g\in G$ il existe $\alpha(g)\in\{-1,1\}$ tel que $g\cdot f=\alpha(g)f$ . On vérifie immédiatement que $\alpha$ doit être un morphisme de groupes.

Premier cas : $\alpha$ est le morphisme trivial. Comme G agit transitivement sur K, on vérifie immédiatement que f est constante donc $\Delta=C$

Deuxième cas : $\alpha=\chi$ . Notons H le sous-groupe d'indice 2 de G. Comme H agit transitivement sur X et sur Y, $f$ est constante sur X et constante sur Y. De plus, pour tout $g\in G-H$ , g envoie X sur Y et $\chi(g)=-1$ , donc la valeur de f sur X est opposée de la valeur de f sur Y. On en déduit que f est proportionnelle à $f_0$ donc que $\Delta=D$ .

Ceci achève la démonstration que C,C',D,D' sont irréductibles sous l'action de G.

Soit $\tilde{G}$ le groupe des isométries du cube. On a $\tilde{G}=\{\pm g/\; g\in G\}\simeq G\times \{-1,1\}$ .

Les sous-espaces $S=C\oplus C'$ et $A=D\oplus D'$ sont les sous-espaces propres de E pour l'action de $-1\in \tilde{G}$ , donc il est clair que la décomposition précédente est encore stable par $\tilde{G}$ , donc que c'est la décomposition en sous-espaces irréductibles sous l'action du groupe des isométries du cube.

35. Le jeudi 8 juillet 2010 à 19:04, par JLT

Solution du no.16
Notons $V_n$ le volume de la boule unité en dimension n, et $\sigma_n$ le volume de la sphère $S^{n-1}\subset \mathbb{R}^n$ . En utilisant les coordonnées "polaires", on a

$V_n=\int_0^1 r^{n-1}\sigma_n\,dr=\sigma_n/n$ , et
$\pi^{n/2}=\int_{\mathbb{R}^n} e^{-||x||^2}\,dx=\sigma_n\int_0^\infty e^{-r^2}r^{n-1}\,dr$ .

On a donc
$V_n=\pi^{n/2}/\int_0^\infty nr^{n-1}e^{-r^2}\,dr$
En intégrant par parties, on obtient $V_n=\pi^{n/2}/\int_0^\infty 2r^{n+1}e^{-r^2}\,dr$ .
Puis, en faisant un changement de variables $t=r^2$ , on trouve $V_n=\frac{\pi^{n/2}}{\Gamma(1+n/2)}.$

Si n est pair, $V_n=\frac{\pi^{n/2}}{(n/2)!}$ .

Si n est impair, $V_n=\pi^{(n-1)/2}/(\frac{1.3.5...n}{2^{(n+1)/2}})=\frac{2^{(n+1)/2}\pi^{(n-1)/2}}{1.3.5...n}$ .

Dans l'exercice, on demande de calculer $V_n/2^n$ .

Pour n=5, on trouve $\pi^2/60$ .

Pour n=10, on trouve $\pi^5/122880$ .

36. Le jeudi 8 juillet 2010 à 19:28, par JLT

Solution du no.17
Soit n=100. On note $V_k$ le volume de la boule unité de dimension k. On veut calculer une valeur approchée à 10% près de

$d=\frac{\int_0^1x(1-x^2)^{(n-1)/2}V_{n-1}\,dx}{\int_0^1 (1-x^2)^{(n-1)/2}V_{n-1}\,dx}=\frac{\int_0^1x(1-x^2)^{(n-1)/2}\,dx}{\int_0^1 (1-x^2)^{(n-1)/2}\,dx}$
$=\frac{1}{(n+1)\int_0^1 (1-x^2)^{(n-1)/2}\,dx}$
L'intégrale $I_n=\int_0^1(1-x^2)^{(n-1)/2}\,dx$ est une intégrale de Wallis. Une intégration par parties donne que $nI_nI_{n-1}$ est constant, donc égal à $\pi/2$ .

Par conséquent, $nI_n^2\le nI_nI_{n-1}=\pi/2$ et $(n+1)I_n^2\ge (n+1)I_{n+1}I_n=\pi/2$ , donc
$\sqrt{\frac{\pi}{2(n+1)}} \le I_n \le \sqrt{\frac{\pi}{2n}}$ .

On en déduit que $\sqrt{\frac{2}{\pi n}}$ est une bonne valeur approchée de d. Pour n=100, d est approximativement égal à 0,08.

Remarque : la méthode de Laplace permet également de trouver une valeur approchée des intégrales de Wallis.

37. Le vendredi 9 juillet 2010 à 16:27, par JLT

Solution du no.40
Si $s\mapsto\gamma(s)$ est une courbe paramétrée par l'abscisse curviligne dans une variété Riemannienne, alors la courbure géodésique est le vecteur $\nabla_{\dot{\gamma}(s)}\dot{\gamma}(s)$ , où $\nabla$ est la connexion de Levi-Civita.

Icil il s'agit de la courbe $\gamma(s)=(s,1)$ , donc il s'agit de calculer $\nabla_XX$ , où $X$ est le champ de vecteurs $\frac{\partial}{\partial x}$ . Par ailleurs, notons $Y=\frac{\partial}{\partial y}$ . Les champs de vecteurs $X$ et $Y$ sont orthogonaux, commutent, et sont de norme $1/y$ .

La connexion de Levi-Civita est caractérisée par la formule
$2\langle \nabla_UV,W\rangle = U.\langle V,W\rangle + V.\langle W,U\rangle - W.\langle U,V\rangle$ , valable pour tout triplet de champs de vecteurs qui commutent deux à deux.

On en déduit $2\langle\nabla_XX,X\rangle=0$ et $2\langle\nabla_XX,Y\rangle=\frac{2}{y^3}$ , donc $\nabla_XX=\frac{Y}{y}$ . On en conclut que la courbure géodésique de la droite y=1 est le vecteur $Y=\frac{\partial}{\partial y}$ .

38. Le samedi 10 juillet 2010 à 22:15, par JLT

Solution du no.36
Soit $f_\lambda(x)=((A-\lambda E)^{-1}x,x)$ . Notons $S_\lambda$ la surface $f_\lambda^{-1}(1)$ . Le gradient de f est $2(A-\lambda E)^{-1}x$ , donc pour tout $x\in S_\lambda$ , le vecteur $\vec{n}_\lambda=(A-\lambda E)^{-1}x$ est normal en $x$ à $S_\lambda$ .

Si $x\in S_\lambda\cap S_\mu$ avec $\lambda,\mu$ distincts, on a $0=f_\lambda(x)-f_\mu(x)=(\lambda-\mu)((A-\lambda E)^{-1}(A-\mu E)^{-1}x,x)=(\lambda-\mu) (\vec{n}_\lambda,\vec{n}_\mu)$ , donc $\vec{n}_\lambda$ est bien orthogonal à $\vec{n}_\mu$ .

39. Le samedi 10 juillet 2010 à 22:33, par MathOMan

Wow ! JLT finira bientôt toute la collection !! Bon, je suis en vacances (et mon cerveau aussi) mais je vais quand même contribuer une petite solution.

Solution du no.33

En coordonnées projectives (X:Y:Z) l'équation de la courbe est X³=YZ². Dans le domaine où $Z\neq0$ la courbe est lisse d'équation x³=y. En revanche si Z=0 alors X=0 et donc la courbe possède un point à l'infini, à savoir (0:1:0). Au voisinage de ce point la courbe a pour équation $\xi^3=\zeta^2$ dans la carte $(\xi,\zeta)=(X/Y,Z/Y)$ . Le point (0:1:0) est donc un cusp (point singulier de la parabole de Neil).

40. Le dimanche 11 juillet 2010 à 12:19, par JLT

Je crois que parmi ceux qui restent, il y en a plus d'exercices difficiles (pour moi) que d'exercices faciles...

Solution du no.20
Notons $t\mapsto x(A,t)$ la solution de ce problème de Cauchy. On a clairement $x(0,t)=\mbox{ch}(t)$ . Notons $y=\frac{\partial x}{\partial A}$ . En dérivant l'équation par rapport à A, on obtient $\ddot{y}=y+{\dot{x}}^2+2A\dot{x}\dot{y}$ , donc si $u(t)$ désigne $y(0,t)$ , on a
$\ddot{u}=u+\mbox{sh}^2(t)=u+\frac{\mbox{ch}(2t)-1}{2}$ .

En cherchant une solution particulière de la forme $a\mbox{ch}(2t)+b$ , on trouve $\frac{\mbox{ch}\,2t}{6}+\frac{1}{2}$ , donc $u$ est de la forme
$u(t)=\alpha \mbox{ch}\,t+\beta\mbox{sh}\,t+\frac{\mbox{ch}\,2t}{6}+\frac{1}{2}$ .
Comme $u(0)=\frac{\partial x}{\partial A}(0,0)=0$ , on a $\alpha=-2/3$ , et comme $\dot{u}(0)=\frac{\partial^2x}{\partial A\partial t}(0,0)=\frac{\partial}{\partial A}\frac{\partial x}{\partial t}(0,0)=0$ , on a $\beta=0$ . Par conséquent,
$u(t)=-\frac{2}{3} \mbox{ch}\,t+\frac{\mbox{ch}\,2t}{6}+\frac{1}{2}$ .

Solution du no.21
Par continuité des racines par rapport aux coefficients, la frontière du domaine de stabilité consiste en l'ensemble des triplets $(a,b,c)$ tels que les racines du polynôme $P(x)=x^3+ax^2+bx+c$ admettent des racines de parties réelles négatives ou nulles, et au moins une racine de partie réelle nulle.

Premier cas : P(0)=0. On cherche les conditions sur a et b pour que $x^2+ax+b=0$ admette deux racines de parties réelles $\le 0$ . Si $\Delta=a^2-4b\ge 0$ , la condition est $-a+\sqrt{\Delta}\le 0$ , ce qui équivaut à $a\ge 0$ et $b\ge 0$ . Si $\Delta<0$ , la condition est $a\ge 0$ . On remarque que si $\Delta<0$ alors on a nécessairement $b\ge 0$ . On en conclut que, lorsque c=0, la condition sur a et b est que $a\ge 0$ et $b\ge 0$ .

Deuxième cas : $P(0)\ne 0$ . Alors P admet deux racines imaginaires pures conjuguées $\pm iy$ . On a
$-iy^3-ay^2+iby+c=0$ , donc $c=ay^2$ et $b=y^2$ , ce qui donne $c=ab$ et $b\ge 0$ . On a alors
$P(x)=x^3+ax^2+bx+ab=(x^2+b)(x+a)$ . Les racines sont de partie réelle $\le 0$ si et seulement si $a\ge 0$ .

Conclusion : la frontière du domaine de stabilité a pour équation
$a\ge 0, b\ge 0, (c=0\mbox{ ou }c=ab)$ .

41. Le dimanche 11 juillet 2010 à 14:19, par JLT

Solution du no.03
Notons $f(z)=z^2+2\bar{z}=x^2-y^2+2x,2(xy-y))$ . On calcule que le jacobien de f vaut $4(x^2+y^2-1)$ donc l'ensemble des points critiques de f est le cercle unité. L'ensemble C des valeurs critiques est l'image par f du cercle unité. Comme $f(\bar{z})=\overline{f(z)}$ et $f(jz)=j^2f(z)$ , C est invariant par la symétrie d'axe des abscisses et par la rotation d'angle $-2\pi/3$ , donc C est invariant par le groupe diédral $D_3$ des isométries du triangle équilatéral.

Il suffit donc de tracer la courbe paramétrée $(x(t),y(t))=(\cos 2t+2\cos t,\sin 2t-2\sin t)$ pour $0\le t\le \pi/3$ en remarquant que $x(t)$ et $y(t)$ sont décroissantes sur cet intervalle, qu'il y a une tangente horizontale au point (3,0) et que la tangente au point $(1,-\sqrt{3})$ a une pente égale à 1. On complète ensuite par symétrie. On obtient une sorte de triangle équilatéral écrasé, inscrit dans le cercle de centre 0 et de rayon 3.

Remarque : le site melusine
melusine.eu.org/syracuse/...
permet de tracer des courbes paramétrées en ligne.

Solution du no.04
On décompose la fraction en éléments simples, et on utilise $\left(\frac{1}{x}\right)^{(n)}=(-1)^n\frac{n!}{x^{n+1}}$ . On trouve
$100!\left(-\frac{1}{x^{101}}+\frac{1}{(x-1)^{101}}+\frac{1}{(x+1)^{101}}\right)$ .

42. Le dimanche 11 juillet 2010 à 14:52, par JLT

Solution du no.30
Si un champ de vecteurs $x\mapsto \vec{v}_x$ s'annule uniquement à l'origine, l'indice de ce champ de vecteurs à l'origine est égal au degré de l'application $x\mapsto \vec{v}_x/||\vec{v}_x||$ de la sphère unité vers elle-même. Comme le degré d'une application est un invariant d'homotopie, et que l'on a une homotopie
$((1-\lambda)(x^4+y^4+z^4)+\lambda(x^2+y^2+z^2),(1-\lambda)(x^3y-xy^3),(1-\lambda)xyz^2))$ entre le champ de vecteurs initial et un champ de vecteurs qui est constant sur la sphère unité (via des champs de vecteurs s'annulant uniquement en l'origine), l'indice est nul.

Solution du no.31
Il s'agit de trouver l'indice par rapport à l'origine du champ de vecteurs $A\left(\begin{array}[c] x\\y\\z\end{array}\right)$ , où A est la matrice $\left(\begin{array}[ccc]0&1&1\\1&0&1\\1&1&0\end{array}\right)$ . Or, A est de déterminant >0, donc est homotope dans $GL(3,\mathbb{R})$ à l'identité. Par conséquent, l'indice du champ de vecteurs est 1.

43. Le dimanche 11 juillet 2010 à 15:32, par JLT

Solution du no.97
Lorsque l'on projette un cube, chaque point du projeté est à la fois le projeté d'un point d'une face qui est "devant" et un point d'une face qui est "derrière". Comme il y a 6 faces, l'espérance recherchée (que nous noterons E) est 3 fois l'espérance de l'aire de la projection d'un carré de côté 1 suivant une projection de direction aléatoire. On se place en coordonnées sphériques de sorte que le carré soit dans le plan horizontal. On note $\varphi$ la latitude. L'aire de la projection du carré est $|\sin\varphi|$ , donc
$E=3\frac{1}{4\pi}\int_{\theta=0}^{2\pi}\int_{\varphi=-\pi/2}^{\pi/2}|\cos\varphi\sin\varphi|\,d\varphi d\theta$
$=\frac{3}{2}\int_{-\pi/2}^{\pi/2}|\cos\varphi\sin\varphi|\,d\varphi=\frac{3}{2}\int_0^{\pi/2}\sin 2\varphi\,d\varphi = 3/2$ .

44. Le dimanche 11 juillet 2010 à 21:13, par JLT

Solution du no.67
La moyenne d'une fonction harmonique sur une sphère est égale à sa valeur au centre de la sphère. D'après l'exercice 66, la valeur cherchée est l'angle solide sous lequel le disque est vu depuis le point (0,0,2), qui est
$\int_{r=0}^1\int_{\theta=0}^{2\pi}\frac{2}{(r^2+4)^{3/2}}rdrd\theta$ . En posant $s=r^2+4$ , ceci vaut
$2\pi\int_4^5\frac{ds}{s^{3/2}}=\pi(\frac{1}{2}-\frac{1}{\sqrt{5}})$ .

45. Le dimanche 11 juillet 2010 à 22:04, par JLT

Solution du no.83
Montrons que toute droite convient.

Si $u$ est un vecteur non nul et $v$ un vecteur quelconque, la distance de $v$ à la droite engendrée par $u$ est $||v||^2-(v.u)^2/||u||^2$ , donc il s'agit de montrer que la forme quadratique $q(u)=\sum_v (v.u)^2$ , où $v$ parcourt les sommets d'un cube (resp. tétraèdre régulier, icosaèdre régulier), est proportionnelle à $||u||^2$ . Or, q est invariante par le groupe des isométries d'un polyèdre régulier. Celui-ci contient un sous-groupe isomorphe à $A_4$ , qui est engendré dans une base orthonormée adéquate par les applications $(x,y,z)\mapsto (y,z,x)$ et $(x,y,z)\mapsto (x,-y,-z)$ . On vérifie immédiatement qu'une forme quadratique $ax^2+by^2+cz^2+dxy+eyz+fzx$ qui est invariante par ces transformations est proportionnelle à $x^2+y^2+z^2$ . CQFD.

Solution du no.84
Notons $P_\varepsilon$ le polynôme caractéristique de la matrice de la forme quadratique. Les longueurs des demi-axes sont $1/\sqrt{\lambda}$ où $\lambda$ sont les racines de $P_\varepsilon$ , donc il s'agit de calculer $-\frac{1}{2}\lambda^{-3/2}\frac{d\lambda}{d\varepsilon}$ en $\varepsilon=0$ .

D'après le calcul de l'exercice 18, on a $P_0(x)=-(x-2)(x-1/2)^2$ . En utilisant la multilinéarité du déterminant, on calcule que $P_\varepsilon(x)=-((x-2)(x-1/2)^2+\frac{\varepsilon}{2}(x-\frac{1}{2})+\frac{\varepsilon^2}{4}(1-x))$ .

Pour $x=2+h$ ( $h$ petit), on a $9h/4+3\varepsilon/4=0$ modulo des termes du second ordre, donc $x=2-\varepsilon/3+o(\varepsilon)$ . On a donc $(\frac{d\lambda}{d\varepsilon})(0)=-1/3$ (pour la valeur propre proche de 2), donc la dérivée en $\varepsilon=0$ de la longueur du demi-axe proche de $1/\sqrt{2}$ est $-1/(12\sqrt{2})$ .

Pour $x=\frac{1}{2}+h$ , on a $-12h^2+4\varepsilon h + \varepsilon^2=0$ modulo des termes d'ordre 3, donc $h=\varepsilon/2+o(\varepsilon)$ ou $h=-\varepsilon/6+o(\varepsilon)$ . Le même raisonnement que plus haut permet d'en déduire que les dérivées en $\varepsilon=0$ des deux longueurs des demi-axes proches de $\sqrt{2}$ sont $-1/(2\sqrt{2})$ et $1/(6\sqrt{2})$ .

46. Le dimanche 11 juillet 2010 à 22:17, par JLT

Arnold Trivium — Solution du no.77
Supposons $\lambda\ne 0$ . En développant $(x+y)^2$ , on voit que $y\mapsto \lambda u(y)+1$ est un polynôme de degré au plus 2, donc $y$ également. Toutes les solutions sont donc de la forme $u(x)=ax^2+bx+c$ . En substituant dans l'équation, on obtient le système
$\left(\begin{array}[ccc]\frac{1}{3}-\lambda&\frac{1}{2}&1\\\frac{1}{2}&\frac{2}{3}-\lambda&1\\\frac{1}{5}&\frac{1}{4}&\frac{1}{3}-\lambda\end{array}\right)\left(\begin{array}[c]a\\b\\c\end{array}\right)=\left(\begin{array}{c}0\\0\\1\end{array}\right)$ , ce qui se résout avec les formules de Cramer en
$(a,b,c)=\frac{1}{(\lambda+1/6)(\lambda^2-\lambda/6-1/180)}(\lambda-1/6,\lambda+1/6,\lambda^2-\lambda-1/36)$
si le dénominateur ne s'annule pas. Si le dénominateur s'annule, on résout le système à la main (ce que j'ai la flemme de faire).

Dans le cas où $\lambda=0$ , le calcul précédent permet de trouver une solution particulière $180(x^2-x+1/6)$ . Les solutions sont somme de cette solution particulière et d'une fonction orthogonale à l'espace des polynômes de degré au plus 2 pour le produit scalaire $\langle f,g\rangle =\int_0^1 f(x)g(x)\,dx$ .

47. Le dimanche 11 juillet 2010 à 22:51, par JLT

Solution du no.85
On détermine un plan en prenant une origine $c=(c_1,\ldots,c_n)$ et deux vecteurs orthonormaux u et v. Le point $c+xu+yv$ appartient au cube si et seulement si $|c_i+u_ix+v_iy|\le 1$ pour tout i. La figure est donc une intersection de n bandes. De plus, elle est nécessairement bornée et convexe. Les différentes figures que l'on obtient dont donc des polygones convexes ayant au plus $2n$ côtés.

(Remarque : je ne sais pas si on attend des réponses plus précises à la question.)

48. Le lundi 12 juillet 2010 à 13:43, par JLT

Solution du no.42
L'application $(\lambda,x,y)\mapsto (\mbox{ch}(\lambda\mbox{argsh}||y||)\frac{x}{||x||},\mbox{sh}(\lambda\mbox{argsh}||y||)\frac{y}{||y||})$ ( $0\le\lambda\le 1$ , $||x||^2-||y||^2=1$ ) définit une rétraction de la surface sur $\{x,\;||x||=1\}=S^{k-1}$ donc les nombres de Betti $b_i$ sont égaux à 1 si $i=0$ ou $i=k-1$ et sont nuls sinon.

L'ensemble $||x||^2\le ||y||^2+1$ est contractile (car étoilé par rapport à l'origine) donc $b_0=1$ et $b_i=0$ pour $i\ge 1$ .

Solution du no.43
Première question :
Il s'agit d'un hyperboloïde à une nappe, compactifié en ajoutant un cercle à l'infini, donc c'est un 2-tore. On a $b_0=b_2=1, b_1=2$ .

Deuxième question :
Les quadriques projectives des questions 1 et 2 sont homéomorphes (car $x^2+y^2-z^2-t^2$ et $xy-zt$ sont des formes quadratiques équivalentes), donc elles ont les mêmes nombres de Betti.

Troisième question :
En coordonnées homogènes on a l'équation $zt=x^2$ . A l'infini on a une droite projective $\{(0:y:z:0)\}$ . La surface est un cylindre parabolique (que l'on peut paramétrer avec les coordonnées $(x,y)$ , donc isomorphe au plan affine) auquel on ajoute une droite projective.
On remarque que $(x:\lambda x^2:x^2:1)$ tend vers $[0:\lambda:1:0]$ donc on voit que la surface est homéomorphe au disque unité quotienté par les relations $i\sim -i$ et $e^{i\theta}\sim e^{i(\pi-\theta)}$ . C'est donc un 2-tore pincé (c'est-à-dire un 2-tore dans lequel on a contracté un cercle en un point), qui a pour nombres de Betti $b_0=b_1=b_2=1$ , $b_i=0$ pour $i\ge 3$ .
En effet, $b_0=1$ car la surface est connexe. $b_1=1$ car le groupe fondamental est visiblement égal à $\mathbb{Z}$ . Pour voir que $b_2=1$ on peut par exemple constater qu'il y a une triangulation comportant trois 0-simplexes, six 1-simplexes et quatre 2-simplexes, donc la caractéristique d'Euler est 3-6+4=1. Or, celle-ci est aussi égale à $\sum (-1)^i b_i$ .

Quatrième question :
Il s'agit de deux cônes circulaires reliés par leurs sommets et recollés à leurs bases, donc c'est encore un tore pincé. Les nombres de Betti sont les mêmes que ci-dessus.

49. Le lundi 12 juillet 2010 à 18:45, par JLT

Solution du no.80
On cherche $\varphi$ satisfaisant $-c\varphi'=(\varphi''+\frac{\varphi^2}{2})'$ .
Il existe K constant tel que $\varphi''+c\varphi+\frac{\varphi^2}{2}=K$ . On en déduit que $\varphi''$ tend vers une limite en l'infini. Celle-ci est nécessairement nulle puisque $\varphi$ tend vers une limite, donc $K=c+1/2$ .

On multiplie par $\varphi'$ et on intègre : $\frac{(\varphi')^2}{2}+\frac{c}{2}\varphi^2+\frac{\varphi^3}{6}-(c+1/2)\varphi$ est constant. On en déduit de même que $\varphi'$ tend vers 0 à l'infini, donc la constante est $-c/2-1/3$ . On factorise alors l'équation précédente en
${\varphi'}^2=\frac{1}{3}(\varphi-1)^2(-3c-2-\varphi)$ . Nécessairement, $c<-1$ . On pose $v^2=-3c-2-\varphi$ . L'équation devient $\frac{2\sqrt{3}\,dv}{-3c-3-v^2}=\pm dx$ . On décompose en éléments simples la fraction rationnelle du membre de gauche, ce qui donne
$\pm (x-x_0)=\frac{1}{\sqrt{-c-1}}\log \left| \frac{v+\sqrt{-3c-3}}{v-\sqrt{-3c-3}}\right|=\frac{2}{\sqrt{-c-1}}\mbox{argth}\frac{v}{\sqrt{-3c-3}}$ .
Ceci permet d'exprimer v en fonction de x, puis $\varphi=-3c-2-v^2$ en fonction de x:
$\varphi(x)=1+\frac{-3c-3}{\mbox{ch}^2\frac{\sqrt{-c-1}}{2}(x-x_0)}$ .

50. Le lundi 12 juillet 2010 à 19:08, par JLT

Solution du no.76
Premier cas : $\lambda\ne 1$ . On a une solution particulière $u_0(x)=(\sin x)/(\lambda-1)$ .
a) Si $\lambda>0$ , les autres solutions de l'équation différentielle sont de la forme $u_0+A\cos\sqrt{\lambda}x+B\sin\sqrt{\lambda}x$ . D'après les conditions au bord, on a A=0 et (B=0 ou $\sqrt{\lambda}\in\mathbb{N}$ ), donc si $\sqrt{\lambda}\notin\mathbb{N}$ , $u_0$ est l'unique solution. Si $\sqrt{\lambda}\in\mathbb{N}$ , les solutions sont de la forme $u_0+B\sin\sqrt{\lambda}x$ donc il y en a une infinité.

b) Si $\lambda\le 0$ on montre de même que $u_0$ est l'unique solution.

Deuxième cas : $\lambda=1$ . Alors $u_0(x)=-(x\cos x)/2$ est une solution de l'équation diférentielle (ne satisfaisant pas les conditions au bord). Les autres solutions son de la forme $u_0+A\cos x+B\sin x$ , mais on voit facilement qu'aucune de ces solutions ne satisfont les conditions au bord.

Conclusion : le nombre de solutions est
- 0 si $\lambda=1$
- infini si $\lambda=2^2,3^2,4^2,\ldots$
- 1 sinon

51. Le lundi 12 juillet 2010 à 19:18, par JLT

Solution du no.13
L'idée est d'utiliser le résultat suivant : soit f une fonction dérivable positive telle que f'=o(f) en $+\infty$ , et telle que $\int_0^\infty f(y)e^y\,dy$ diverge. Alors $\int_0^a f(y)e^y\,dy ~f(a)e^a$ .

Démonstration : $\int_0^a f(y)e^y\,dy=f(a)e^a-f(0)-\int_0^a f'(y)e^y\,dy$ . Or, $f'(y)e^y=o(f(y)e^y)$ donc $\int_0^a f'(y)e^y = o(\int_0^a f(y)e^y\,dy$ , ce qui démontre le résultat.

Ici, on effectue le changement de variables $y=x\ln x$ . On a $dx=dy/(1+\ln x)$ donc $f(y)=1/(1+\ln x)$ et $f'(y)/f(y)=(df/dx)(dx/dy)/f=-1/x$ , donc les hypothèses sont bien satisfaites.

L'intégrale est donc approchée par $10^{10}/(1+\ln 10)$ . Or, tout physicien sait que $\ln 10\simeq 2,3$ et que 1+2,3=3,3 est environ égal à 10/3, donc l'intégrale vaut environ $3.10^9$ .

Vérification sur www.solvemymath.com/onlin...
3 057 488 912

On peut bien sûr encadrer plus précisément l'intégrale $\int_0^a f(y)e^y\,dy$ (où $a\ln a=10$ ) en calculant la somme de Riemann correspondant à la subdivision $x\in [1,2], [2,3],\ldots, [9,10]$ , ou bien en majorant $|\int_0^a f'(y)e^y\,dy|$ par $\int_0^b |f'(y)|e^y\,dy + |f'(b)|e^a$ .

Solution du no.14
On utilise la méthode de Laplace. La fonction $f(x)=(x^4+4x+4)^{-1}$ atteint un unique maximum en x=-1. On a $f(-1+y)=1-6y^2+o(y^2)$ . On peut en déduire que l'intégrale est approchée par $\int_{-\infty}^{+\infty}e^{-600y^2}\,dy=\sqrt{\pi/600}$ .

(On pourrait estimer l'erreur de façon plus rigoureuse, mais j'ai la flemme et de plus l'énoncé n'incite pas à le faire car il demande une approximation grossière).

52. Le mardi 13 juillet 2010 à 21:54, par JLT

Solution du no.15
Je donne ici seulement le moyen pour estimer une telle intégrale, mais je ne prouve pas que l'erreur est de moins de 5%.

Préliminaire : $\int_{-\infty}^\infty \cos x^2\,dx = \int_{-\infty}^\infty \sin x^2\,dx=\sqrt{\pi/2}$ .
En effet, soit $f(z)=e^{iz^2}$ . L'intégrale de f sur la ligne brisée allant de 0 à R, puis jusqu'à R(1+i), puis jusqu'à 0, est nulle car f est holomorphe sur $\mathbb{C}$ .
Si $z=R+iy$ , on a $|f(z)|=e^{-2Ry}$ , donc $|\int_{R}^{R+iR} f(z)\,dz|\le \int_0^Re^{-2Ry}\,dy=O(1/R)$ tend vers 0 lorsque R tend vers l'infini.
On en déduit que $\int_0^\infty f(x)\,dx=\int_0^\infty f((1+i)t)(1+i)\,dt=(1+i)\int_0^\infty e^{-2t^2}\,dt=\frac{1+i}{2\sqrt{2}}\int_{-\infty}^{\infty}e^{-t^2}\,dt=(1+i)\frac{\sqrt{\pi}}{2\sqrt{2}}$ .
En prenant les parties réelles et imaginaires, et en utilisant le fait que $\cos x^2$ et $\sin x^2$ sont paires, on obtient le résultat.

De là, on tire grâce à la formule $\cos(u+v)=\cos u\cos v -\sin u\sin v$ que si b>0, alors $\int_{-\infty}^\infty \cos(a+bx^2)\,dx=(\cos a-\sin a)\sqrt{\frac{\pi}{2b}}$ .

Posons maintenant $f(x)=100(x^4-x)$ . La dérivée s'annule uniquement en $\alpha=2^{-2/3}$ . On voit que l'intégrale est "concentrée" autour de $\alpha$ . En effet, en posant $y=f(x)$ on a par exemple
$\int_1^\infty cos f(x)\,dx=\int_0^\infty \cos y\,\frac{dy}{100(4x(y)^3-1)}$ où $x(y)$ est l'unique réel $\ge \alpha$ tel que $f(x(y))=y$ . En intégrant par parties, on voit que $|\int_1^\infty cos f(x)\,dx| \le |1/(100(4x(0)-1)|=1/300$ .

Près de $\alpha$ , on a $\cos f(x)\simeq f(\alpha)+\frac{f''(\alpha)}{2}(x-\alpha)^2$ , donc l'intégrale est approchée par $(\cos f(\alpha)-\sin f(\alpha))\sqrt{\frac{\pi}{f''(\alpha)}}\simeq -0,09$ .

53. Le mercredi 14 juillet 2010 à 11:45, par JLT

Solution du no.02
Il suffit de calculer un développement limité à l'ordre 7 du numérateur et du dénominateur. La limite vaut 1.

(En fait j'ai triché car j'ai eu la flemme de calculer à la main, alors j'ai utilisé le logiciel Maxima...)

54. Le mercredi 14 juillet 2010 à 11:59, par JLT

Solution du no.23
Je ne pense pas qu'on puisse trouver une expression explicite de x en fonction de t. En tout cas je n'en ai pas trouvé (ce qui ne veut rien dire car je n'ai pas étudié les équations différentielles au-delà du niveau bac+2) et Maxima non plus. On peut néanmoins résoudre partiellement l'équation :

Posons $y=x^{-2}$ . L'équation devient $2y\ddot{y}-3{\dot{y}}^2-2\dot{y}+4=0$ . On pose $s=\dot{y}$ . Notons $y'=dy/ds$ . On a
$\frac{y'}{y}=\frac{2s}{3s^2+2s-4}$ , ce qui s'intègre en
$x^{-2}=y=C|s+\frac{1-\sqrt{13}}{3}|^{\frac{13-\sqrt{13}}{39}}|s+\frac{1+\sqrt{13}}{3}|^{\frac{13+\sqrt{13}}{39}}$ .
De plus, comme $\frac{ds}{dt}=\ddot{y}=\frac{3s^2+2s-4}{2y}=\frac{3}{2C}|s+\frac{1-\sqrt{13}}{3}|^{\frac{26+\sqrt{13}}{39}}|s+\frac{1+\sqrt{13}}{3}|^{\frac{26-\sqrt{13}}{39}}$ , ceci permet d'obtenir t comme l'intégrale d'une certaine fonction de s.

55. Le mercredi 14 juillet 2010 à 12:31, par JLT

Solution du no.25
Première question :
L'unique point d'équilibre est (0,0). Au voisinage de 0, le système linéarisé a pour valeurs propres $-j, -j^2$ qui ont des parties réelles >0 donc c'est un point d'équilibre répulsif.

On se demande si les courbes intégrales sont bornées ou peuvent tendre vers l'infini. Lorsque y est grand, le système différentiel devient approximativement $\dot{x}=y, \dot{y}=-y-x$ , qui est un système différentiel linéaire avec pour valeurs propres $j,j^2$ . En diagonalisant la matrice, on trouve que si (x,y) est solution de ce système linéaire, alors $z=x-jy$ satisfait $\dot{z}=jz$ .

Revenons au système initial. Posons $z=x-jy$ . On calcule que $\dot{z}=jz-2j\sin y$ , donc $|(d/dt)(e^{-jt}z)|\le 2e^{t/2}$ . En intégrant entre 0 et t, en en déduit que $|e^{-jt}z|\le |z(0)|+4e^{t/2}$ . Comme $|e^{jt}|=e^{-t/2}$ , on en tire que $|z(t)|\le |z(0)|e^{-t/2}+4$ . Ceci signifie que le point $(x,y)$ se rapproche à une vitesse exponentielle de l'intérieur de l'ellipse $x^2+y^2+xy\le 4$ .

Deuxième question :
(Solution à la physicienne! Après tout ce sont des exercices pour physiciens...)
Notons $V(x)=-x^2+x^4/4+x^3/3$ le potentiel. Le terme avec $\varepsilon$ correspond à un frottement. Il y a deux puits de potentiel en x=-2 et x=1, et un équilibre instable en x=0. Sauf dans des cas très particuliers, x(t) tend vers l'un des puits de potentiel.

Notons $E=\frac{y^2}{2}+V(x)$ l'énergie. On a $\dot{E}=-\varepsilon y^2$ . Or, pour l'oscillateur harmonique, sur une période l'énergie cinétique moyenne est égale à la moitié de l'énergie totale, donc $\dot{E}$ est de l'ordre de $-4\varepsilon (E-E_0)$ où $E_0$ est l'énergie minimale (au creux de potentiel).

Ceci signifie que la particule oscille autour du point d'équilibre stable avec une amplitude de l'ordre de $Ce^{-2\varepsilon t}$ .

56. Le jeudi 15 juillet 2010 à 10:03, par JLT

Solution du no.79
Il y a une erreur de frappe, je suppose que l'énoncé correct était $\varphi(+\infty)=0$ .

Supposons qu'une telle fonction existe. On a $-c\varphi'=\varphi-\varphi^2+\varphi''$ . Comme $0\le\varphi\le 1$ , $\varphi''+c\varphi'=\varphi^2-\varphi\le 0$ donc $e^{cx}\varphi'(x)$ est décroissante.

Comme $\varphi(+\infty)<\varphi(-\infty)$ , $\varphi$ ne peut pas être croissante, donc il existe $a$ tel que $\varphi'(a)<0$ . Comme $e^{cx}\varphi'(x)\le e^{ca}\varphi'(a)<0$ pour tout $x\ge a$ , on en déduit que si $c\le 0$ alors $\varphi'(x)\le \varphi'(a)$ , ce qui entraîne $\varphi(+\infty)=-\infty$ . Impossible.

On en déduit que $c>0$ .

On multiplie l'équation par $\varphi'$ :
$(\varphi-\varphi^2)\varphi'+\varphi'\varphi''=-c{\varphi'}^2$ , ce qui s'intègre en $(\varphi^2/2-\varphi^3/3)+{\varphi'}^2/2+K=-c\int{\varphi'}^2$ .
En $+\infty$ , le membre de gauche est minoré tandis que le membre de droite tend vers une limite négative ou nulle (éventuellement $-\infty$ ). On en déduit que les deux membres ont une limite finie lorsque $x\to+\infty$ , donc $\varphi'$ admet une limite en $+\infty$ . Comme $\varphi$ a également une limite, $\varphi'$ tend nécessairement vers 0.

On raisonne de même en $-\infty$ . Le membre de droite tend vers une limite finie ou bien vers $+\infty$ . Dans le deuxième cas, comme $\varphi^2/2-\varphi^3/3$ est borné, ${\varphi'}^2$ tend vers $+\infty$ , ce qui contredit le fait que $\varphi$ admet une limite. Donc le membre de droite tend vers une limite finie, ce qui entraîne que ${\varphi'}^2$ également, et on en déduit comme plus haut que $\varphi'$ tend vers 0 en $-\infty$ .

En intégrant entre $-\infty$ et $+\infty$ la relation $\varphi-\varphi^2=-\varphi''-c\varphi'$ , on voit que l'intégrale $\int_{-\infty}^{+\infty}\varphi-\varphi^2$ converge. De plus,
$e^{cx}\varphi'(x)=e^{ca}\varphi'(a)-\int_a^x(\varphi-\varphi^2)$ . On choisit $a$ de sorte que $e^{ca}\varphi'(a)\ne \int_a^{+\infty} \varphi-\varphi^2$ . Un tel $a$ existe car si pour tout $a$ on avait $e^{ca}\varphi'(a)= \int_a^{+\infty} \varphi-\varphi^2$ alors, en faisant $a\to -\infty$ , on aurait $\varphi'(a)\to +\infty$ , ce qui est impossible.

Revenons à $e^{cx}\varphi'(x)=e^{ca}\varphi'(a)-\int_a^x(\varphi-\varphi^2)$ . Le membre de droite tend vers une limite non nulle quand $x\to +\infty$ , que l'on notera $-A$ . On a donc $\varphi'(x)\sim -Ae^{-cx}$ en $+\infty$ . En intégrant entre $x$ et l'infini, on en déduit que $\varphi(x)\sim (A/c)e^{-xc}$ . Comme $\varphi''=-c\varphi'-(\varphi-\varphi^2)$ , on a $\varphi''=(Ac-A/c)e^{-cx}+o(e^{-cx})$ , ce qui s'intègre en $\varphi'(x)\sim (-A/c)(c-1/c)e^{-cx}$ . On a donc la relation $(-A/c)(c-1/c)=-A$ , ce qui équivaut à $c=c-1/c$ . Impossible.

Conclusion : aucune valeur de c ne convient.

57. Le jeudi 15 juillet 2010 à 11:29, par JLT

Solution du no.34
Il s'agit d'une surface de révolution $(r^2-2)^2+z^2=1$ . Elle ressemble vaguement à un tore. Les géodésiques des surfaces de révolution sont traitées dans la plupart des livres de géométrie Riemannienne, ou sur certains sites internet tels que geothalg : www.geothalg.ulg.ac.be/ge...

Je ne pense pas qu'on puisse trouver une équation explicite des géodésiques. Cependant, on peut observer que les courbes $\theta=\mbox{const.}$ sont des géodésiques, ainsi que les deux cercles z=0. Les autres géodésiques s'enroulent autour de la surface, comme l'indique le théorème de Clairaut (voir le site indiqué plus haut).

58. Le jeudi 15 juillet 2010 à 18:47, par JLT

Solution du no.29
Notons $f(z)$ le champ de vecteurs. On vérifie d'abord que les points singuliers sont bien isolés. En effet, la différentielle de f vaut $df=({\bar{z}}^2+4z^3)dz+2\bar{z}(z+4{\bar{z}}^2)d\bar{z}$ . Ceci s'annule si et seulement si ${\bar{z}}^2=-4z^3$ et $\bar{z}(z-16z^3)=0$ , c'est-à-dire $z=0$ ou $z=-1/4$ . Or, $f(-1/4)\ne 0$ , et $z=0$ est un zéro isolé car au voisinage de 0 on a $f(z)\sim z{\bar{z}}^2$ .

Par ailleurs, comme $f(z)={\bar{z}}^4(2+(z/\bar{z})^4+z/{\bar{z}}^2)$ , les zéros de $f$ sont tous dans le disque unité.

Soit $h:\mathbb{R}_+\to \mathbb{R}_+^*$ une fonction $C^\infty$ telle que $h(t)=1$ pour tout $t\le 1$ , et $h(t)=1/t^4$ pour $t\ge2$ . Soit $g(z)=h(|z|)f(z)$ . On considère $g(z)$ comme un champ de vecteurs sur la sphère de Riemann. D'après les considérations qui précèdent, le théorème de Poincaré-Hopf (fr.wikipedia.org/wiki/Th%... s'applique: la somme des indices des points singuliers de g (y compris 0 et $\infty$ ) est égale à la caractéristique d'Euler de la 2-sphère qui vaut 2.

Au voisinage de 0, $g(z)=f(z)$ est homotope à $h(z)=z{\bar{z}}^2$ . Comme $h(\varepsilon e^{i\theta})/|h(\varepsilon e^{i\theta})|=e^{-i\theta}$ , l'indice en 0 vaut -1.

Pour calculer l'indice en l'infini, on utilise le changement de cartes $u=1/z$ . Comme $du=-(dz)/z^2$ , le champ de vecteurs $g$ vu dans la nouvelle carte est égal à $-g(z)/z^2=-|u|^4 f(1/u)u^2=-u^4/(\bar{u})^2(2+k(u))$ avec $|k(u)|<2$ pour $|u|<1$ . Ceci est homotope au champ de vecteurs $-u^4/{\bar{u}}^2$ qui a pour indice 6.

Conclusion : la somme des indices du champ de vecteurs $f(z)$ en les points singuliers autres que l'origine vaut -3.

59. Le vendredi 16 juillet 2010 à 14:43, par JLT

Solution du no.75
Je pense qu'il y a une faute de frappe, c'est sans doute un A et non un Q.

On cherche des solutions de la forme $A=\cos x \cos\alpha t$ . La première équation donne $(9-\alpha^2)A=-2B$ . En reportant dans la deuxième, on trouve $4=(9-\alpha^2)(6-\alpha^2)$ , ce qui donne $\alpha=\pm\sqrt{5}$ ou $\alpha=\pm\sqrt{10}$ .

Par linéarité, $A(x,t)=(a\cos\sqrt{5}t + b\cos\sqrt{10}t)\cos x$ sont des solutions. On a $-2B=(4a\cos\sqrt{5}t-b\cos\sqrt{10}t)\cos x$ . Les conditions initiales imposent que $a+b=1$ et $4a-b=0$ , donc $a=1/5, b=4/5$ .

On a donc trouvé une solution $A=((1/5)\cos\sqrt{5}t + (4/5)\cos\sqrt{10}t)\cos x$ et $B=((-2/5)\cos\sqrt{5}t + (2/5)\cos\sqrt{10}t)\cos x$ .

C'est l'unique solution (pour le voir il suffit de regarder la transformée de Fourier par rapport à x).

60. Le vendredi 16 juillet 2010 à 15:02, par JLT

Solution du no.95
Ici je n'ai pas de solutino mathématiquement rigoureuse (et d'ailleurs je doute qu'on puisse trouver une valeur exacte de N sans effectuer de calcul numérique sur ordinateur). Je vais donc seulement donner une estimation de N, mais je ne sais pas majorer l'erreur car je n'ai pas assez fait de probas dans ma scolarité.

Soit $X=X_1+\cdots+X_N$ , où les $X_i$ sont des variables aléatoires indépendantes de même loi uniforme sur $\{0,\ldots,5\}$ . On calcule aisément que $E(X)=5N/2$ et $V(X)=20N/3$ . Lorsque N est grand, on assimile X à une variable Gaussienne. Si m est la moyenne et $\sigma$ l'écart-type d'une variable aléatoire Gaussienne, on calcule au moyen d'un ordinateur que $P(|X-m|<2,17\sigma)\simeq 0,97$ . On choisit les N/10 joueurs sur un intervalle centré en le N/2-ième joueur (puisque 5N/2 est congru à N/2 modulo N). a probabilité que l'un de ces joueurs gagne est environ $P(|X-5N/2|)<N/20$ (on néglige les cas où $|X-5N/2|>N/2$ ), qui doit valoir environ 0,97 donc $N/20=2,17\sqrt{20N/3}$ . On en tire que N vaut environ 12500.

En assimilant X à une Gaussienne, on estime que la probabilité que le meneur gagne est de l'ordre de
$2.\frac{1}{2\pi.(20N/3)}\int_{N/2}^{N/2+1} e^{-x^2/(2.20N/3)}\,dx$ , ce qui se comporte comme $Ce^{-3N/160}$ .

On peut sûrement être plus précis (montrer que c'est un équivalent, et calculer C), mais comme l'énoncé demande le "comportement", cela ne m'incite pas à aller plus loin.

61. Le vendredi 16 juillet 2010 à 15:09, par JLT

Solution du no.01
Je ne sais pas si on peut vraiment "résoudre" cet exercice, mais on peut aisément passer du graphe d'une fonction à celle de sa dérivée en utilisant la correspondance suivante :

1) f croissante <--> f' positive
2) f décroissante <--> f' négative
3) f atteint un extremum local en x <--> f' change de signe en x
4) f convexe <--> f' croissante
5) f concave <--> f' décroissante
6) x est un point d'inflexion pour f <--> f' change de sens de variation
7) f admet une direction asymptotique oblique de pente a en $\pm\infty$ <--> f' tend vers a en $\pm\infty$ .

62. Le vendredi 16 juillet 2010 à 15:53, par JLT

Solution du no.08
Dans cet exercice, on supposera que les différentielles de $f_1=x+\cdots v+$ , $f_2=x^2+\cdots +v^2$ et $f_3=x^3+\cdots +v^3$ sont linéairement indépendantes en tout point de la surface que nous noterons S(afin que ce soit effectivement une surface). Ceci signifie qu'en tout point de S, il existe un mineur 3x3 non nul. Or, les mineurs 3x3 sont des déterminants de Van Der Monde, donc cela signifie qu'en tout point de S, trois des coordonnées sont distinctes.

Soit $f=x^4+\cdots +v^4$ . Les points critiques de f sont les points de S en lesquels df est combinaison linéaire des $df_i$ . En raisonnant comme plus haut, les points critiques sont ceux pour lesqueles $x,\ldots,v$ prennent exactement trois valeurs distinctes.

Premier cas : l'une des valeurs est prise 3 fois, par exemple u=v=x. Notons $(x_0,y_0,z_0,x_0,x_0)$ un tel point. Le triplet $(x_0,y_0,z_0)$ satisfait le système (S)
$\left\{\begin{array}{l} 3x_0+y_0+z_0=a\\3x_0^2+y_0^2+z_0^2=b\\3x_0^3+y_0^3+z_0^3=c\end{array}\right.$
Notons m le nombre de solutions de (S) satisfaisant $x_0<y_0<z_0$ ou $y_0<z_0<x_0$ , et M le nombre de solutions vérifiant $y_0<x_0<z_0$ .

Notons $S_i$ les sommes de Newton et $\sigma_i$ les fonctions symétriques élémentaires de $x,y,z$ .

On a $f=S_4+u^4+v^4=u^4+v^4+\frac{4}{3}S_1S_3-S_1^2S_2+\frac{1}{6}S_1^4+\frac{S_2^2}{2}$ .
Tous calculs faits, on a $\frac{\partial^2 f}{\partial u^2}=8(3u^2-\sigma_1u+\sigma_2)=8\varphi'(u)$ où $\varphi(X)=(X-x)(X-y)(X-z)$ , donc $\frac{\partial^2 f}{\partial u^2}(x_0,y_0,z_0)=8(x_0-y_0)(x_0-z_0)$ . De même, $\frac{\partial^2 f}{\partial v^2}(x_0,y_0,z_0)=8(x_0-y_0)(x_0-z_0)$ . Enfin, $\frac{\partial^2 f}{\partial u\partial v}=4(u^2+v^2+uv-(u+v)S_1+\sigma_2)$ , qui vaut $4(x_0-y_0)(x_0-z_0)$ .

La matrice Hessienne est définie positive ssi $x_0<y_0,z_0$ ou $x_0>y_0,z_0$ , définie négative sinon. On a un minimum local dans le premier cas et un maximum local dans le deuxième cas.

Comme, étant donnés trois réels $x_0,y_0,z_0$ , il y a $2C_5^3=20$ manières de les affecter à 5 variables de sorte que $x_0$ soit répété 3 fois, on a trouvé 20m minima locaux et 20M maxima locaux.

On peut résoudre le système (S) en éliminant $y_0$ et $z_0$ . On obtient une équation du 3e degré dont $x_0$ est solution, donc on sait que $1\le m+M\le 3$ , mais il ne me paraît difficile de calculer simplement m et M en fonction de a,b,c.

Deuxième cas : 2 valeurs sont prises 2 fois. On est amené à résoudre le système (S') suivant :
$\left\{\begin{array}{l} 2x_0+2y_0+z_0=a\\2x_0^2+2y_0^2+z_0^2=b\\2x_0^3+2y_0^3+z_0^3=c\end{array}\right.$
Notons m' le nombre de solutions de (S) satisfaisant $x_0<z_0<y_0$ , et K le nombre de solutions vérifiant $z_0<x_0<y_0$ ou $x_0<y_0<z_0$ .

On calcule qu'en un tel point, $\frac{\partial^2 f}{\partial u\partial v}=0$ , $\frac{\partial^2 f}{\partial u^2}=8(x_0-y_0)(x_0-z_0)$ , $\frac{\partial^2 f}{\partial v^2}=8(y_0-x_0)(y_0-z_0)$ . La matrice Hessienne est diagonale avec 2 valeurs >0 si $x_0<z_0<y_0$ , et deux valeurs de signes opposés sinon.

Comme $5 C_4^2=30$ , on trouve comme plus haut 30m' minima locaux supplémentaires et 30K points col. On sait que m'+K est compris entre 1 et 3 mais on ne peut pas en dire plus.

Finalement, on a au total :
20m+30m' minima locaux
20M maxima locaux
30K points col.
On sait que $1\le m+M\le 3$ , $1\le m'+K\le 3$ , $M\ge 1$ , $m+m'\ge 1$ (pour ces deux dernières inégalités on utilise que toute fonction continue sur un compact atteint ses bornes). Je ne vois pas comment déterminer plus précisément m,m',M et K en fonction de a,b,c (mais je sais que ces valeurs dépendent réellement de a,b,c).

63. Le vendredi 16 juillet 2010 à 21:05, par JLT

Solution du no.37
Je pense qu'il y a une erreur d'énoncé car la surface est un cylindre, et la courbure de Gauss est nulle. J'imagine que la formule correcte est $z^4+(x^2+y^2-1)(2x^2+3y^2-1)=0$ . On se convainc aisément que cette surface est difféomorphe au 2-tore, qui a pour caractéristique d'Euler zéro. D'après le théorème de Gauss-Bonnet, l'intégrale de la courbure de Gauss est nulle.

64. Le samedi 17 juillet 2010 à 10:03, par JLT

Solution du no.94
On suppose que $a<b$ (sinon on peut montrer que la particule tend presque sûrement vers l'infini). Notons $\lambda=a/b$ .
Notons $c=1-a-b$ la probabilité de rester sur place.
Notons $X_n$ la position de la particule à l'instant n, et $u_n(k)=P(X_n=k)$ . On a $u_{n+1}(0)=bu_n(1)+(b+c)u_n(0)$ , et $u_{n+1}(k)=au_n(k-1)+cu_n(k)+bu_n(k+1)$ .

Montrons par récurrence sur n que pour tout $k\ge 0$ , $u_n(k+1)\le \lambda u_n(k)$ .

Pour n=0 c'est évident. Supposons l'assertion vraie pour l'entier n.

Pour tout $k\ge 1$ , $u_{n+1}(k+1)=au_n(k)+cu_n(k+1)+bu_n(k+2)$
$\le\lambda(au_n(k-1)+cu_n(k)+bu_n(k+1))=\lambda u_{n+1}(k)$ .

Pour k=0, $u_{n+1}(1)=au_n(0)+cu_n(1)+bu_n(2)\le au_n(0)+\lambda (cu_n(0)+bu_n(1))$
$=\lambda((b+c)u_n(0)+bu_n(1))=\lambda u_{n+1}(0)$ .

Ceci achève la récurrence.

On a $u_{n+1}(0)-u_n(0)=bu_n(1)-au_n(0)\le 0$ , donc la suite $(u_n(0))_{n\in\mathbb{N}}$ est décroissante. Comme elle est positive, elle converge.

En utilisant les relations $bu_n(1)=u_{n+1}(0)-(b+c)u_n(0)$ et $bu_n(k+1)=u_{n+1}(k)-cu_n(k)-au_n(k-1)$ pour tout $k\ge 1$ , on voit par récurrence immédiate que pour tout k, la suite $(u_n(k))_{n\in\mathbb{n}}$ converge, et que si $p_k$ désigne sa limite, alors les relations
$bp_1=ap_0$ et $bp_{k+1}=(1-c)p_k-ap_{k-1}=(a+b)p_k-ap_{k-1}$ sont satisfaites. On en déduit aisément par récurrence que $p_k=p_0\lambda^k$ .

Pour tout $n$ , on a $u_n(k)\le u_n(0)\lambda^k$ donc $1\le \sum_{k=0}^\infty u_n(k)\le u_n(0)/(1-\lambda)$ , ce qui implique $u_n(0)\ge 1-\lambda$ . En faisant tendre n vers l'infini, on obtient l'inégalité $p_0\ge 1-\lambda$ .

Inversement, comme pour tout k on a $1\ge P(X_n\le k)=u_n(0)+\cdots + u_n(k)$ , par passage à la limite on obtient $1\ge p_0+\cdots+p_k$ , donc $1\ge \sum_i p_i=p_0/(1-\lambda)$ .

En combinant les inégalités précédentes, on a $p_0=1-\lambda$ . On déduit que $p_k=(1-\lambda)\lambda^k$ pour tout $k$ .

On a $\sum_{n\ge 1} n\lambda^n=\lambda \frac{d}{d\lambda}\sum\lambda^n=\lambda/(1-\lambda)^2$ , donc $E(X)=\sum_{n\ge 1}(1-\lambda)n\lambda^n=\lambda/(1-\lambda)=a/(b-a)$ .

On a $\sum_{n\ge 1} n^2\lambda^n=\lambda\frac{d}{d\lambda}\sum n\lambda^n = \lambda(1+\lambda)/(1-\lambda)^3$ , donc $E(X^2)=\lambda(1+\lambda)/(1-\lambda)^2=a(a+b)/(b-a)^2$ .

65. Le samedi 17 juillet 2010 à 15:39, par JLT

Solution du no.35
Je ne pense pas qu'on puisse trouver une équation paramétrique ou cartésienne explicite de la développante, donc je ne sais pas jusqu'à quel point on peut être précis. Ici, je cherche simplement la présence d'asymptotes.

Comme $ds=\sqrt{1+(dx/dy)^2}dy=\sqrt{1+\frac{1}{9|y|^{4/3}}}dy=(1+\frac{1}{18|y|^{4/3}}+o(|y|^{-4/3}))dy$ . En intégrant, on voit que $s=y+f(s)$ où f est une fonction admettant des limites (finies) en $\pm\infty$ .

Comme $\vec{r}+(c-s)\dot{\vec{r}}=(x,x^3)+(c-s)\frac{(1,3x^2)}{\sqrt{1+9x^4}}$
$=(x,x^3)-(y+f(s)+o(1))(3x^2)^{-1}(1-\frac{1}{18x^4}+o(x^{-4}))(1,3x^2)$
$=(2x/3-f(s)/3+o(1),-f(s)+o(1))$ .

On en conclut que la développante admet deux asymptotes horizontales. De plus, elle est tangente à la parabole cubique (là où s=c) et la recoupe en un autre point.

66. Le samedi 17 juillet 2010 à 17:30, par JLT

Arnold Trivium — Solution du no.26
A translation près, on peut supposer que le point critique du potentiel est en x=0 et que U(0)=0. On alors $U(x)=(ax^2)/2+o(x^2)$ où a est non nul. On peut résoudre l'équation différentielle $\ddot{x}=-ax-k\dot{x}$ . Dans le cas où $a>0$ , il s'agit de l'oscillateur harmonique avec amortissement. En résolvant l'équation, on voit que les solutions sont des sortes de sinusoïdes descendantes, situées dans la zone au-dessus de la parabole $E=ax^2/2$ et tangentes en une infinité de points à cette parabole, et tendant vers le sommet (0,0). L'énergie décroît avec le temps, tandis que la position x oscille de part et d'autre de la position d'équilibre avec une amplitude qui tend vers 0.

Dans le cas a>0, on peut de même résoudre l'équation différentielle linéaire du second ordre et constater que E varie de $+\infty$ vers $-\infty$ , x varie de $\pm\infty$ vers [tex]\mp \infty[\tex] et que la trajectoire dans le plan (x,E) a des branches paraboliques (sauf que bien sûr, quand |t| est grand, l'approximation n'est plus valable car on s'éloigne de la position d'équilibre).

67. Le samedi 17 juillet 2010 à 17:58, par JLT

Solution du no.06
On peut tracer la courbe ici : melusine.eu.org/syracuse/...
Lorsque l'on change le signe de t, (x,y) est transformé en (-x,y) donc le graphe est symétrique par rapport à l'axe des ordonnées. Il suffit d'étudier la courbe pour $t\ge 0$ . On calcule les dérivées de x et de y par rapport à t, et on constate que x et y sont croissantes sur $[0,6^{-1/2}]$ et décroisantes sur $[6^{-1/2},\infty[$ . Comme x' et y' changent de signe en $t_0=6^{-1/2}$ , et comme $y'(t)/x'(t)$ tend vers $t_0$ lors que $t\to t_0$ il y un point de rebroussement en $(x(t_0),y(t_0))=(\frac{4}{3\sqrt{6}},\frac{1}{12})$ , et la demi-tangente a pour pente $t_0$ .

Au voisinage de $(0,0)$ , on a $x\sim 2t$ et $y\sim t^2$ , donc la courbe ressemble à la parabole $y=x^2/4$ .

Quand $t\to+\infty$ , on a $y\sim-3\frac{|x|^{4/3}}{4^{1/3}}$ donc il y a une branche parabolique d'axe Oy.

Enfin, la courbe coupe l'axe des abscisses au point de paramètre $1/\sqrt{3}$ et l'axe des ordonnées au point de paramètre $1/\sqrt{2}$ . Il est aisé avec ces données de tracer le graphe de la courbe.

68. Le samedi 17 juillet 2010 à 18:45, par JLT

Solution du no.24
J'ai trouvé les définitions de la stabilité de Lyapunov sur Wikipedia : fr.wikipedia.org/wiki/Sta...

Considérons le système $\dot{x}=y, \dot{y}=-x^3-y^3$ .

Le système linéarisé est $\dot{x}=y, \dot{y}=0$ , les droites horizontales ne passant pas par 0 sont des courbes intégrales donc le système linéarisé est instable.

Montrons que le système initial est asymptotiquement stable.
Soit $E=\frac{y^2}{2}+\frac{x^4}{4}$ . On a $\dot{E}=-y^4$ donc l'énergie est décroissante. Comme elle est positive, elle converge quand $t\to +\infty$ . Ceci entraîne que x et y sont bornées, et par récurrence toutes les dérivées de x et de y par rapport à t sont bornées. Or, $\int_0^{+\infty} y^4(t)\,dt=E(0)-E(+\infty)<+\infty$ , et comme la dérivée de $y^4$ est bornée, il est facile d'en déduire que $y^4$ , donc $y$ , tend vers 0. Or, $x^4=4E-2y^2$ , donc $x^4$ tend vers une limite, et par conséquent $x$ aussi. Comme $\dot{y}=-x^3-y^3$ , $\dot{y}$ admet une limite en l'infini, qui est nécessairement nulle puisque y ne tend pas vers l'infini. Donc $x^3$ tend vers 0, ce qui équivaut à ce que $x\to 0$ .

Finalement, on a prouvé que le système est asymptotiquement stable alors que le système linéarisé est instable.

69. Le samedi 17 juillet 2010 à 22:00, par JLT

Arnold Trivium — Solution du no.07
Quitte à changer de coordonnées, on se ramène à l'ellipse $x^2+y^2/a^2=1$ . Le nombre de normales que l'on peut mener d'un point $(u,v)$ à l'ellipse est le nombre de solutions de l'équation $0=(u-\cos\theta)(-\sin\theta)+(v-a\cos\theta)(a\cos\theta)$
$=z^{-2}(1-a^2)/(4i)(z^4-1+cz^3+dz)$ , où $d=2(u+iav)/(1-a^2)$ et $c=-\bar{d}$ . On calcule que le discriminant de $z^4-1+cz^3+dz$ vaut $27(c^4+d^4)+4(cd)^3-6(cd)^2+192(cd)+256=27(c^2-d^2)^2+4(4+cd)^3$ . En remplaçant c et d par leur expression en u et v, on calcule que la zone où le nombre de normales est maximal est donnée par l'équation
$-27X^2Y^2+(1-(X^2+Y^2))^3>0$ , où $X=u/(1-a^2)$ et $Y=av/(1-a^2)$ . Cette zone est l'intérieur d'une astroïde.

70. Le samedi 17 juillet 2010 à 22:53, par JLT

Epilogue.

No.27 : je ne comprends pas l'énoncé. Je ne sais pas ce qu'est $z$ .

No.28 : je ne comprends pas l'énoncé car je ne sais pas ce qu'est le cercle de Larmor, et je n'ai jamais passé mes vacances à Larmor (www.larmor-plage.com).

No.32 : je ne suis pas sûr de comprendre l'énoncé, et je ne vois pas comment procéder.

No.38 : je ne sais pas calculer l'intégrale par la force brute, et je ne comprends pas ce qu'elle représente géométriquement.

No.41 : je n'ai pas trouvé, et mon intuition ne me permet pas de deviner la réponse.

No.44 : je ne comprends pas l'énoncé. Je ne vois même pas où sont les auto-intersections (peut-être que j'ai raté quelque chose d'évident).

No.51 : j'ai essayé en changeant de contour dans le plan complexe mais ça n'a pas abouti.

No.58 : je ne vois pas comment procéder. A la rigueur je pense pouvoir minorer cette valeur de t mais je ne vois pas de moyen de la calculer exactement.

No.68 : la condition devrait être que la sphère est une équipotentielle, mais quand j'écris l'équation je n'arrive pas à intégrer.

No.69 : je ne comprends pas ce qu'il faut calculer, ni quelles sont les hypothèses. Considère-t-on que l'orbite de la lune est inclinée par rapport à l'écliptique ou non?

No.70 : je ne sais pas comment on calcule la capacité d'un condensateur connaissant la forme de celui-ci.

No.73 : je ne sais pas comment commencer.

No.74 : j'imagine qu'il faut commencer par écrire le Laplacien en coordonnées hypersphériques. J'ai trouvé
$\sum_{i=1}^{n-1}\frac{1}{(\sin\theta_1\cdots\sin\theta_{i-1})^2\sin\theta_i}\frac{\partial}{\partial\theta_i}(\sin\theta_i\frac{\partial}{\partial \theta_i})$ . J'imagine qu'il faut ensuite généraliser les harmoniques sphériques en dimensions supérieures, mais je n'ai pas le courage de me lancer dedans.

Bref, selon Arnold mon niveau de connaissances en mathématiques est compris entre 80% et 85% du strict minimum nécessaire pour un étudiant de physique. Ceci devrait néanmoins être suffisant pour préparer des candidats à l'agrégation de mathématiques.

71. Le lundi 27 décembre 2010 à 18:43, par MathOMan

Concernant le No.28 : D'après ce que je viens d'apprendre par un physicien à la retraite (mon père) les cercles de Larmor n'appartiennent pas à une plage bretonne mais au physicien-mathématicien irlandais Sir Joseph Larmor (1857-1942).

Et concernant la No.44 j'ai lu un peu ces définitions. Je propose donc la solution suivante. Peut-être un spécialiste pourra me corriger si c'est faux.

Arnold Trivium — Solution du no.44

La réponse est seize.

Le nombre d'intersections C.C' de deux courbes algébriques (sans composante commune) C et C' sur une surface compacte est le cardinal de $C\cap C'$ où on compte chaque point avec sa multiplicité correspondante. Pour généraliser cette définition on déclare comme nombre d'auto-intersections C.C de C le nombre C.C' où C' est une courbe obtenue de C par une légère perturbation dans une diréction générique. Dans le plan il s'agit simplement de translater la courbe dans une direction. (Sur une surface plus générale il faut prendre C' linéairement équivalente à C.) On peut alors montrer que C.C' ne dépend pas du choix de C'.

Dans le cas de l'exercice on est dans le plan. Je prends donc

$C : \;\;x^4 + y^4 = 1, \;\;\;\;\; C' : \;\; (x+1)^4 + y^4 = 1.$

Par le théorème de Bézout l'indice d'auto-intersection est 16. Ceux qui ne connaissent pas ce théorème peuvent calculer à la main comme suit. Par soustraction des deux équations on trouve :

$4x^3+6x^2+4x+1 = 0.$

Ce polynôme possède trois racines et comme y⁴=1-x⁴ en trouve 12 points d'intersection pour les courbes affines. Il reste à trouver les points d'intersection à l'infini. Les équations en coordonnées homogènes (X:Y:Z) telles que (x,y)=(X/Z,Y/Z) sont

$C : \;\;X^4 + Y^4 = Z^4, \;\;\;\;\; C' : \;\; X^4 +4X^3Z+6X^2Z^2+4XZ^3+ Y^4 = 0.$

On voit immédiatement que le point (0:1:0) n'est pas dans C. Donc pour les points d'intersection à l'infini on a Z=0 et X non-nul. Avec t=Y/X on obtient 1+t⁴=0, donc quatre points d'intersection à l'infini. Au total donc seize.

72. Le mardi 28 décembre 2010 à 11:53, par JLT

Du coup, le no. 28 est assez simple.

Arnold Trivium — Solution du no.28

Notons $\vec{\tau}$ le vecteur unitaire tangent et $\vec{n}$ le vecteur tel que $\frac{d\tau}{ds}=\frac{1}{R}\vec{n}$ , où $R\ge 0$ est le rayon de courbure (qui est aussi le rayon du cercle de Larmor). Si $M$ est la position de la particule, alors le centre de courbure $\Omega$ est défini par $\Omega=M+R\vec{n}=M+\frac{mv}{|q|B}\vec{n}$ . On dérive par rapport à t:

$\frac{d\Omega}{dt}=\vec{v}+\frac{1}{B}\frac{d}{dt}(\frac{mv}{|q|}\vec{n})-\frac{mv}{|q|B^2}(\vec{\nabla}B\cdot\vec{v}) \vec{n}$ .

Les deux premiers termes s'annulent mutuellement (lorsque $B$ est constant le centre de courbure est fixe), donc le centre du cercle de Larmor dérive dans la direction $(\Omega M)$ , et on a $\frac{d\Omega}{dt}=-\frac{mv}{|q|B^2}(\vec{\nabla}B\cdot\vec{v}) \vec{n}$ .

73. Le mardi 28 décembre 2010 à 14:30, par JLT

J'ai parlé trop vite, la solution est incomplète.

Supposons pour se fixer les idées que la charge est négative. Alors la particule décrit approximativement des cercles de rayon R dans le sens trigonométrique. Le temps nécessaire pour parcourir un tour est $\delta T=2\pi R/v$ .
On se place en coordonnées polaires par rapport au centre du cercle à l'instant t.
On a $\frac{d\Omega}{dt}=-R\frac{\vec{\nabla}B}{B}\cdot\vec{v}\,\vec{n}$ .

Or, au premier ordre (on considère que le champ magnétique varie peu sur des distances de l'ordre du rayon du cercle de Larmor, c'est-à-dire que $R||\vec{\nabla} B||/B$ est petit), le second membre est approximativement

$\frac{vR}{B}\left( -\frac{\partial B}{\partial x}\sin\theta + \frac{\partial B}{\partial y}\cos\theta\right) \left(\begin{array}{c} \cos\theta\\ \sin\theta\end{array}\right)$

On intègre pour $\theta\in [0,2\pi]$ et on divise par $\2\pi$ pour obtenir la vitesse moyenne :

$\frac{vR}{2B}\left(\begin{array}{c}\frac{\partial B}{\partial y}\\ -\frac{\partial B}{\partial x}\end{array}\right)=-\frac{vR}{2B}\vec{z}\wedge \vec{\nabla}{B}=\frac{mv^2}{2qB^3}\vec{B}\wedge \vec{\nabla}{B}.$

J'espère ne pas avoir fait d'erreur de calcul...

74. Le mardi 28 décembre 2010 à 18:18, par MathOMan

Voilà, après le grand travail pendant les vacances d'été, c'est reparti ! Peut-être on finira le trivium grâce aux vacances de Noël ;-)

Arnold Trivium — Solution du no.32

Le système d'équations différentielles linéaires $\ddot x=-4x, \ddot y=-9y$ possède comme solution générale dans l'espace de phases

$(x(t),\dot x(t),y(t),\dot y(t))=(a_1 \cos(2t+t_1),a_1 \sin(2t+t_1),a_2 \cos(3t+t_2),a_2 \sin(3t+t_1)),$

où t_k sont des réels et a_k des réels non-nuls (petits si on veut des petites oscillations comme dans l'énoncé — mais ça n'a pas d'importance). Cette trajectoire de phase représente deux nœuds : après la période $2\pi$ la courbe $(x(t),\dot x(t))$ se referme sur elle-même après ayant fait deux tours tandis que $(y(t),\dot y(t))$ se referme après trois tours. D'après mon intuition naïve, le nombre d'enlacement entre ces deux nœuds devrait donc être 2 × 3 = 6. (Ou encore -6 si l'orientation ou les signes de a_k sont choisis autrement.)

Arnold parle d'une surface d’énergie totale. Mais c'est plutôt une hypersurface (espace de dimension 3) dans l'espace de phases de dimension 4 dans laquelle les nœuds se trouvent. Son équation est E = cte où E est la somme de l'énergie cinétique et du potentiel :

$E = \frac{\dot x^2+\dot y^2}2+2x^2+\frac92y^2.$

Cette hypersurface d’énergie totale est donc une 3-sphère.

75. Le mercredi 29 décembre 2010 à 09:33, par JLT

Du coup, grâce au lien (c'est le cas de le dire) sur Wikipedia concernant le nombre d'entrelacement, l'exercice 38 devient facile.

Arnold Trivium — Solution du no.38

Je suppose qu'il y avait des fautes de frappe et que les courbes sont

1) Le cercle unité du plan $(\cos\alpha,\sin\alpha,0)$ , que l'on notera $C_1$ , et

2) La courbe $(2\cos^2\beta,\frac{1}{2}\sin\beta,\sin 2\beta)=(1+\cos 2\beta,\frac{1}{2}\sin\beta,\sin 2\beta)$ , que l'on notera $C_2$ .

On observe que pour tout $t\in [0,1/2]$ , les courbes $C_1$ et $(1+\cos 2\beta,t\sin\beta,\sin 2\beta)$ ne se coupent pas. En effet, si le point $M=(1+\cos 2\beta,t\sin\beta,\sin 2\beta)$ était sur $C_1$ , on aurait $\sin 2\beta=0$ , donc $1+\cos 2\beta\in \{0,2\}$ . Dans le premier cas, on aurait $M=(0,\pm t,0)\notin C_1$ et dans le deuxième cas $M=(2,0,0)\notin C_1$ .

Comme le nombre d'entrelacement est un invariant d'homotopie, on peut remplacer $C_2$ par la courbe $C_3$ paramétrée par $(1+\cos 2\beta,0,\sin 2\beta)$ qui est un cercle dans un plan perpendiculaire, passant par le centre de $C_1$ , et parcouru deux fois. En faisant une figure, on voit que l'intégrale de Gauss est égale à $-8\pi$

76. Le vendredi 7 janvier 2011 à 15:16, par MathOMan

Restent non-résolus : 27, 41, 51, 58, 68, 69, 70, 73 et 74.

Ajouter un commentaire

Pourquoi ne pas lire aussi :

Exercice d'arithmétique

Par Mathoman, vendredi 10 septembre 2010 à 10:07 - Exo, enigme, casse-tête - Tags

Après une longue absence je viens de faire un peu le ménage dans les commentaires du billet précédent sur les exercices de la liste de Vladimir Arnol'd et je me suis rendu compte que PB y a posé un petit problème que toute le monde a oublié dans la déferlante de solutions (dues pour la plupart à JLT). Le voilà, dans un billet à lui tout seul !

Exercice de PB : calculer la signature de la (multiplication par 541 modulo 1223).

3 commentaires

Approximation d'une intégrale

Par Mathoman, mercredi 16 juin 2010 à 19:39 - Exo, enigme, casse-tête - Tags

Un ami m'a envoyé une belle collection d'exercices dont je parlerai bientôt sur ce blog (c'est ici). L'une des questions est simplement :

Calculer la moyenne de sin¹⁰⁰(x) avec une précision de 10%.

Je suppose qu'il faut comprendre calculer la moyenne sur un intervalle de période (par exemple entre 0 et pi).
Selon l'auteur de cette liste de problèmes, un étudiant qui ne sait pas faire cet exercice en cinq minutes n'aurait aucune maîtrise des mathématiques... Qu'en est-il de vous ? :-)

Et pour rallonger un peu ce billet, voici deux belles phrases.

Algebriquement parlant, Mr M. est execrable, mais Mr G. est (x+1)ecrable.
— Edgar Alan Poe

Même le nombre le plus fort a besoin des nuls : 100000000.
— Zarko Petan

5 commentaires

Vladimir Arnold Trivium - conclusion

Par Mathoman, lundi 3 janvier 2011 à 13:10 - Enseigner les maths - Tags

Avant les vacances d'été j'avais écrit un billet avec les exercices du Trivium mathématique de Vladimir Arnold. Grâce aux efforts estivaux de certains lecteurs, notamment de JLT, presque toute question a trouvé sa solution (sauf les 27, 41, 51, 58, 68, 69, 70, 73, 74). Quelle conclusion peut-on tirer ?

D'abord ce trivium est loin d'être trivial. Il apprend de l'humilité à beaucoup parmi nous, enseignants souvent spécialisés dans certains domaines, et nous rappelle qu'on a la mémoire courte, c'est-à-dire qu'on a tendance à oublier des choses si on ne les utilise/enseigne plus. Deuxièmement, on apprend à apprécier l'outil Wikipédia pour chercher des définitions ou clarifications de certaines notions. Je crois que j'aurais fait mes études plus facilement si Wikipédia avait déjà existé ; mais il y a encore dix ans il fallait aller à la bibliothèque, passer beaucoup de temps à ne rien trouver ou encore trouver des articles et livres où la notion recherchée apparaissait englobée par 200 pages de définitions ou théorèmes...

Mais laissons le dernier mot à l'auteur du Trivium lui-même : en fait, Arnold a écrit un Mathematical Trivium bis dans lequel il résume certaines réactions à son premier Trivium. En plus il y a aussi son texte sur l'enseignement des mathématiques et la vidéo suivante sur les mathématiques expérimentales :

7 commentaires

Einstein a écrit

Par Mathoman, vendredi 8 mai 2009 à 11:23 - Maths et société - Tags

Le Musée de l'histoire de la science à Oxford possède une collection de tableaux noirs qu'on a oublié d'effacer. Comme par exemple celui-ci d'Albert Einstein :

Je suis touché par l'écriture un peu infantil de ce grand génie. Malheureusement je ne comprends pas grande chose de ce qu'il a noté... Et pourquoi d'une ligne à l'autre la fraction $\frac{P_0-P}{P}$ change-t-elle en $\frac{P_0-P}{P_0}$ ? Peut-être un physicien peut nous éclairer !

3 commentaires

Question de codimension en algèbre linéaire

Par Mathoman, lundi 11 mai 2009 à 21:59 - Exo, enigme, casse-tête - Tags

Je collectionne constamment des exercices de maths intéressants et accéssibles aux élèves niveau prépa ou licence. On en trouve beaucoup dans les livres, sur internet, sur les vieilles feuilles d'exercices de ses propres professeurs... et quelques fois en invente soi-même ! Voici une question intéressante qui m'est venue le week-end dernier. La solution que j'ai trouvée ne nécessite pas de grand théorème, il faut seulement bien maîtriser ses connaissances élémentaires en algèbre linéaire :

Quel est le plus grand entier k tel que tout sous-espace affine de codimension k dans l'espace des matrices n x n contient une matrice inversible ?

Rappel : la codimension d'un sous-espace est la différence entre la dimension de l'espace ambiant et la dimension du sous-espace. Autrement dit, c'est le nombre d'équations nécessaires pour décrire le sous-espace (car chaque équation enlève un degré de liberté). Par exemple, dans l'espace habituel à trois dimensions la codimension d'une droite est 2, celle d'un plan est 1.

6 commentaires

Concevoir la notion d'application

Par Mathoman, mardi 6 janvier 2009 à 19:02 - Apprendre les maths - Tags

Je me rappelle qu'au début de mes études de mathématiques, parfois une simple question de formalisme pouvait me poser des problèmes. Par exemple, j'avais du mal à jongler entre différents points de vue d'une notion a priori simple comme celle d'application. Voici quelques lignes qui pourraient sembler bêtes aux initiés, mais comme les livres expliquent rarement ce genre de choses en détail elles peuvent être utiles à ceux qui y sont confrontés pour la première fois — et notamment aux élèves et étudiants d'aujourd'hui qui, lors de leur parcours scolaire, ne rencontrent plus assez de théorie des ensembles.

Considérons une application (synonyme de fonction) d'un ensemble X dans un ensemble Y.

$f\;:\; X \;\longrightarrow \;Y\,,\;\; x \; \longrightarrow\;f(x)\,.$

(Désolé, la deuxième flèche devrait commencer par un pied mais mon plug-in LaTeX ne le permet pas.)

Si vous venez de passer le bac, vous avez déjà une notion intuitive de ce que c'est une application. Mais les mathématiciens possèdent plusieurs autres points de vue pour concevoir cet objet — et chacun a sa raison d'être.

Point de vue y en fonction de x.
C'est le point de vue habituellement enseigné au collège et au lycée. On conçoit x comme variable et y comme l'image qui change en fonction de x.
Le schéma mental est le suivant.
L'ensemble de départ X est représenté horizontalement, l'ensemble d'arrivée Y est représenté verticalement. La donnée de l'application f revient à la donnée de son graphe $\Gamma \subset X\times Y$ constitué des couples (x,f(x)), où x parcourt X.
En disant x parcourt X, on adopte donc bien l'idée que la variable est x.
Point de vue collection d'éléments de Y.
On peut aussi écrire l'application f en forme de famille $(f(x))_{x\in X}$ . On oublie donc de spécifier l'ensemble d'arrivée Y.
En général, une famille $(y_j)_{j\in J}$ dans Y n'est rien d'autre qu'une application

$y\;:\; J \;\longrightarrow \;Y\,,\;\; j \; \longrightarrow\;y_j\,,$

où l'ensemble de départ J est appellé l'ensemble d'indices ; très souvent il n'a pas d'importance et peut être remplacé par un autre ensemble de même cardinal. Ce qui compte dans ce point de vue c'est simplement la collection des images de l'application.
Dans certaines situations un bon choix de l'ensemble d'indices peut raccourcir les écritures. Par exemple, si $(b_j)_{j\in J}$ est une base d'un K-espace vectoriel E, alors tout vecteur v de E se décompose comme combinaison linéaire
$v=\sum_{j\in J} \lambda_j\, b_j\:,$
où $(\lambda_j)_{j\in J}$ est une famille de scalaires presque tous nuls (c'est-à-dire l'application $\lambda\;:\; J \;\longrightarrow \;K\,$ est nulle sauf en un nombre fini de points ; cela est nécessaire pour pouvoir prendre la somme). Mais si on conçoit la base non comme une famille de vecteurs mais comme un sous-ensemble B de l'espace E, alors on peut la prendre elle-même comme ensemble d'indices et écrire simplement
$v=\sum_{b\in B} \lambda_b\, b\:.$
Point de vue les fibres en fonction de y.
Pour chaque y dans Y on appelle fibre de f en y (ou ensemble de niveau y) l'ensemble de tous les antécédents de y, noté

$f_y\;=\;f^{-1}(\{y\:\})\:=\:\{\:x\in X\; :\; f(x)=y\:\} \,.$

Connaître une application revient à connaître la collection de ses fibres. C'est donc y qu'on considére comme variable. On s'aide du schéma mental suivant.

L'espace de départ est projeté sur l'espace d'arrivée. L'application est injective (resp. surjective resp. bijective) si et seulement si chaque fibre possède au plus (resp. au moins resp. précisément) un élément.

Une conséquence naturelle du point de vue des fibres est la factorisation canonique, que nous allons expliquer ci-dessus et dont la quintessence se résume ainsi :

L'ensemble des fibres non-vides d'une application est une partition de l'ensemble de départ et a le même cardinal que l'image de l'application.

Factorisation canonique

Nous nous proposons de montrer que toute application est la composée d'une surjection, d'une bijection et d'une injection. Soit donc f une application de X vers Y. On considère son image

$\tilde{Y} = f(X)\:\subset\:Y$

et l'espace des fibres

$\tilde{X} = \{\,f^{-1}(\{y\})\:|\: y\in \tilde{Y}\,\}\:\subset\:{\scr P}(X).$

Ainsi l'espace des fibres est le quotient de X par la relation d'équivalence ~ qui est définie par x ~ x' si et seulement si f(x) = f(x'). Il est clair que $\tilde{X}$ et $\tilde{Y}$ sont en bijection. Plus précisément il existe une surjection $\pi$ , une bijection $\tilde{f}$ et une injection $j$ tel que le diagramme suivant commute.

Factorisation canonique d'une fonction, comment comprendre les applications

En effet, il suffit de prendre pour $\pi$ la projection canonique sur le quotient X/~, c'est-à-dire l'application qui à chaque x dans X associe la fibre de f en f(x) ; puis pour j l'injection naturelle, et enfin pour $\tilde{f}$ l'application qui envoie une fibre sur l'unique élément dans Y qui est son image par f. Il est alors évident que f est la composée

$f= j\circ \tilde{f}\circ \pi$ .

Un avant-goût de la suite

Concevoir une application comme la collection de ses fibres est très fréquent en topologie, géométrie algébriques et théorie des singularités. On fait varier un point dans l'espace d'arrivée pour observer, dans l'espace de départ, la manière dont varie la fibre au-dessus de ce point. Un exemple très basique est l'application

$f\;:\; \mathbb{R}^3 \;\longrightarrow \;\mathbb{R}\,,\;\; (x,y,z) \; \longrightarrow\;ax+by+cz\,,$

où a,b,c sont des réels fixés non tous nuls. La collection des fibres est constituée de plans parallèles. Il s'agit donc d'un feuilletage de l'espace $\mathbb{R}^3$ par plans (comme un feuilleté). Les fibres se ressemblent toutes ; on a même ce qu'on appelle une fibration globalement triviale.

Plus généralement, si f est une fonction différentiable et si on fait varier le point dans l'espace d'arrivée sans toucher les valeurs critiques, alors localement les fibres se ressemblent toutes (fibration localement triviale). En revanche, si on passe par une valeur critique alors la nature des fibres peut changer. Par exemple si on traverse la valeur critique 0 de l'application

$g\;:\; \mathbb{R}^2 \;\longrightarrow \;\mathbb{R}\,,\;\; (x,y) \; \longrightarrow\;x^2+y^2\,,$

dans le sens décroissant, alors la fibre est d'abord un cercle, puis dégénère en un point et, enfin, devient vide — une catastrophe a lieu au sens de la théorie des catastrophes de René Thom.

Tout ça devient plus intéressant dans le complexe. Les fibres de

$g\;:\; \mathbb{C}^2 \;\longrightarrow \;\mathbb{C}\,,\;\; (x,y) \; \longrightarrow\;x^2+y^2\,,$

sont des surfaces réelles (courbes complexes ou surfaces de Riemann). Et au lieu de traverser la valeur critique 0, on peut la contourner avec un petit lacet dans le plan complexe et observer la déformation de cette surface le long du lacet. Evidemment à la fin on retrouve la même surface qu'au début du lacet, mais lors du trajet certaines caractéristiques se sont déplacés continûment et ont échangés leurs places... (monodromie).

aucun commentaire

Evaluation par QCM dans l'enseignement supérieur

Par Mathoman, lundi 7 juin 2010 à 15:00 - Enseigner les maths - Tags

Dans mon dernier billet sur l'enseignement des mathématiques je parlais du système américain et allemand des devoirs maison hébdomadaires. Je me félicite du succès de ce billet : en effet, les responsables de l'enseignement des maths en cycle préparatoire à l'école d'ingénieurs Estaca l'ont lu et ont décidé la mise en place de ce système à partir de la rentrée prochaine.

Aujourd'hui j'aimerais parler d'une autre idée pour rendre plus efficace le contrôle des acquis des étudiants : les questionnaires à choix multiples. Traditionnellement nous, les matheux, nous n'aimons pas les QCM. Nous considérons les mathématiques comme une sorte d'art où le chemin du raisonnement choisi et la grâce avec laquelle on danse sur ce chemin, c'est-à-dire le style de rédaction, sont aussi importants que le résultat à trouver. Et cela ne peut pas être évalué par un QCM. — C'est vrai. Or quand nous corrigeons les partiels en premier cycle nous faisons souvent l'expérience que très peu d'étudiants savent rédiger correctement une suite d'idées. Et la remarque suivante montre que ce phénomène perdure même dans les semestres supérieurs : L’utilisation des hypothèses données dans l’énoncé doit être signalée au moment opportun et non en vrac en début de question, afin de montrer l’articulation du raisonnement (extrait du rapport du jury de l'agrégation 2009).
Il y a donc un décalage entre nos attentes et les résultats. Et ce n'est pas étonnant car le système des TD actuel n'apprend une rédaction cohérente. Comme le professeur de TD ne peut pas contrôler l'écrit de chacun, les étudiants ne font que recopier une rédaction exemplaire au tableau — ce qui est déjà une bonne chose mais ne suffit point, ça serait comme si on voulait apprendre à jouer le violon en écoutant Gidon Kremer. On revient donc au problème déjà cité de l'efficacité des TD...

Alors à quoi bon d'évaluer les étudiants par des choses sur lesquelles ils n'ont pas eu l'occasion de s'entraîner ? J'ai donc décidé, pour ma part, de faire désormais l'évaluation en forme de QCM (dans les établissements qui n'ont pas mis en place un système de correction de devoirs maison). Mon premier tel examen 100% QCM peut être consulté ici.

Quelles sont les compétences mathématiques qu'on peut évaluer par un QCM ? A mon avis, un bon pourcentage des méthodes au programme d'un premier cycle en école d'ingénieur ou en tronc commun de L1 : dériver, intégrer, systèmes linéaires, équations différentielles linéaires, etc. D'après ce que j'ai vu c'est déjà suffisant pour trier les bons et les mauvais étudiants ;-)

Recherche de collaborateurs

Maintenant je viens avec une proposition concrète : qui a envie de participer à établir une base d'exercices en ligne en forme de QCM ? Qui est-ce qui a déjà de l'expérience en ce domaine (peut-être avec WIMS) et souhaite la partager ? L'idée serait la suivante.

Une grande base de questions serait disponibles en ligne pour que les étudiants puissent s'entraîner chez eux.
Une autre partie de questions serait reservée aux épreuves que les étudiants passent dans les salles d'ordinateur le jour de l'examen.
Les résultats étant calculés automatiquement il n'y aura plus de travail de correction ni erreur d'évaluation possible.
Une fois la base d'exercices créée et assez grande, on peut la rentabiliser et organiser des évaluations très fréquentes...
Les exercices ne devraient pas forcément être interactives, originales ou d'une grande valeur pédagogique en e-learning (comme souvent dans WIMS), car ils serviraient uniquement à évaluer, l'enseignement en TD restant inchangé.

11 commentaires

Maths tordues ou tortues ?

Par Mathoman, vendredi 17 octobre 2008 à 13:45 - Sujets hors sujet - Tags

Définition (selon Wikipédia) : Un Gömböc (mot hongrois) est un corps homogène tridimensionnel convexe comportant un unique point stable et un unique point instable d'équilibre. Posé n'importe comment, il revient toujours à la même position.

La question de trouver un tel corps fût posée par le mathématicien russe Vladimir Arnold et était résolue l'année dernière par deux mathématiciens hongrois. La vidéo suivante montre que certaines tortues ont une carapace qui ressemble à un Gömböc.

Et pour finir avec la même espèce animal voici un très beau dessin connexe (dessiné d'un seul trait) par un artiste de Vanuatu (république en Océanie), spécialisé en dessins de sable. Il part d'une simple grille de référence, donc avec un cahier d'école on devrait pouvoir y arriver... Tout le monde peut s'y entraîner durant des leçons ou séminaires ennuyeux (-;

aucun commentaire

Groupes et compagnie

Par Mathoman, vendredi 7 janvier 2011 à 08:29 - Exo, enigme, casse-tête - Tags

Un magma est un ensemble G muni d'une loi de composition interne ¤.
Si en plus cette loi est associative, c'est-à-dire (x¤y)¤z = x¤(y¤z) pour tous x,y,z dans G, alors on dit que (G,¤) est un demi-groupe.
Et si en plus il existe un élément neutre e dans G, c'est-à-dire e¤x = x¤e = x pour tout x dans G, alors on dit que (G,¤) est un monoïde.
Enfin, si chaque élément x de G possède un neutralisant x' dans G, c'est-à-dire x¤x' = x'¤x = e, alors on dit que (G,¤) est un groupe.

On dit aussi le symétrique de x pour l'élément neutralisant x' de x. Si la loi est notée par une addition on le note souvent -x (opposé) et si la loi est notée par une multiplication on le note souvent x^-1 (inverse).

Exemples :

Considérons la loi de l'addition habituelle de nombres. Muni de cette loi l'ensemble des naturels strictements positifs N*={1,2,3,...} est un semi-groupe. Il manque l'élément neutre 0 ; on l'ajoute et on obtient le monoïde N={0,1,2,3,...}. Il manque les neutralisants (les opposés) -1, -2, -3, ... ; on les ajoute et on obtient le groupe des entiers Z={0,±1,±2,±3,...}.
Considérons la loi de la multiplication habituelle de nombres. Muni de cette loi l'ensemble des naturels N est un monoïde, son élément neutre étant 1. Que faut-il ajouter ou enlever pour en faire un groupe ? D'abord on remarque que 0 multiplié avec tout nombre donne 0, donc jamais 1, autrement dit on ne pourra jamais trouver un neutralisant de 0 (on ne peut pas diviser par zéro...). Il faut donc enlever le 0, on trouve N*. Ensuite il faut ajouter les inverses : l'union de N* et de l'ensemble des 1/n où n parcourt N*, est-il un groupe ? Non, pas encore, car il faut aussi s'assurer que les produits restent dedans et donc on doit en fait ajouter toutes les fractions de la forme m/n avec m et n dans N*. On trouve le groupe multiplicatif Q*⁺ des rationnels strictement positifs.
De même l'ensemble des nombres rationnels non nuls Q* est un groupe.
Il existe des loi internes non-associatifs. L'ensemble Z muni de la soustraction est un magma (mais pas un demi-groupe). L'ensemble R³ muni du produit vectoriel
(x₁, x₂, x₃) × (y₁, y₂, y₃) = (x₂y₃-x₃y₂, x₃y₁-x₁y₃, x₁y₂-x₂y₁)
en est un autre.

Pour résumer, un groupe est un ensemble muni d'une loi interne associative, possédant un élément neutre et tel que chaque élément a un neutralisant. Il s'agit alors de vérifier ces trois axiomes pour montrer qu'un objet proposé est un groupe. Beaucoup d'exercices sont de ce type et très souvent ce sont de simples vérifications mécaniques, permettant au débutant de se familiariser avec la notion de groupe. La rédaction de la réponse à la question suivante m'a pris un peu plus de temps, à savoir toute la durée d'un examen que j'ai surveillé hier — pas terrible de réussir un seul exo pendant que les étudiants doivent en faire cinq ;-) mais évidemment cet exo ne faisait pas partie de l'examen...

Exercice : On définit x¤y := x(y²+1)^½+y(x²+1)^½. L'ensemble des réels muni de cette loi est-il un groupe ?

Toutes les solutions sont acceptées... en particulier celles utilisant la force brute du logiciel de calcul formel Maple car j'aimerais bien savoir si Maple arrive à faire ça. J'ai essayé de forcer Maple mais il ne voulait pas ; soit ça dépasse ses capacités, soit ça dépasse mes compétences maple-istiques.

19 commentaires

Diamond signs et graffiti - de Donald Knuth à John Nash, passant par Jackson Pollock... (nouvelles photos ajoutées)

Par Mathoman, lundi 22 décembre 2008 à 16:06 - Sujets hors sujet - Tags

Pas besoin de présenter Donald Knuth aux mathématiciens. Il est actuellement le seul computer scientist qui figure dans le fameux Peoples Archive. Dans les années 1980 Knuth a fait un grand don au monde: le logiciel libre TeX, fruit de son travail de nombreuses années sur le traitement de texte. Aujourd'hui TeX et son cousin LaTeX sont devenus les standards de l'édition scientifique. Par exemple tous les fichiers PDF sur ce blog sont faits avec LaTeX.

Sur la page personnelle de Don Knuth on trouve des rubriques inhabituels, comme ses IFAQ (Infrequently Asked Questions), et plein d'humour, comme ses Expecting a check from me? ou don't click here. En somme, Don Knuth est ce que les américains appellent un véritable "nerd". Et sa page la plus nerdy est celle-ci : Diamond Signs. Elle contient une galérie de photos de panneaux rares de signalisation routière. Ca m'a donné l'idée de faire une collection similaire, car à défaut d'être génial comme lui je veux au moins être un nerd !

Depuis une année, quand je me promène à vélo dans les rues de Paris, je prends avec mon téléphone portable des photos d'un certain type de graffiti. Dans tous les arrondissements je vois régulièrement des graffiti sur les trottoirs qui font penser à l'action painter Jackson Pollock, surnommé "Jack the Dripper" pour sa fameuse technique de dripping.

J'ignore qui est la personne à l'origine de cet hommage parisien à Jackson Pollock. Si j'avais de l'imagination (mais je n'en ai pas), je n'y verrais même pas de l'art — j'interpréterais ces signes mystérieux comme un codage secret utilisé par des espions, terroristes ou extra-terrestres pour préparer un grand complot dans notre belle capitale... comme le fait le mathématicien John Nash interprété par l'acteur Russell Crowe dans le film Un homme d'exception.

Galérie graffiti sur les trottoirs à Paris


MathOMan, collectionneur de photos des graffiti de trottoir	119 boulevard Diderot 75010 Paris	boulevard de la Chapelle (Pont SNCF) 75018 Paris

Place Mazas 75012 Paris	53 boulevard Diderot 75012 Paris	75 boulevard Richard Lenoir 75011 Paris

4 rue Dahomey 75011 Paris	90 avenue Parmentier 75011 Paris	48 boulevard Richard Lenoir 75011 Paris

Place des Vosges 75004 Paris	34 boulevard Richard Lenoir 75011 Paris	105 quai de Jemmapes 75010 Paris

123 boulevard Diderot 75012 Paris	191 quai de Valmy 75010 Paris	quelque part (adresse oubliée...)

18 rue Trousseau 75011 Paris	21 boulevard de Ménilmontant 75020 Paris	280 boulevard Voltaire 75011 Paris

54 rue Trousseau 75011 Paris	77 boulevard Diderot 75012 Paris	281 boulevard Voltaire 75011 Paris

55 boulevard Diderot 75012 Paris	259 boulevard Voltaire Quasiment devant ma porte...	Place des Vosges 75004 Paris

Envie de jouer un peu à "Jack l'égoutteur" mais sans risquer un procès de la mairie de Paris ? Défoulez-vous virtuellement sur le très surpenant site www.jacksonpollock.org !!!

Cliquez sur l'image

3 commentaires

Catégories

La collection d'exercices de Vladimir Arnol'd

Commentaires

Ajouter un commentaire

Pourquoi ne pas lire aussi :

Exercice d'arithmétique

Approximation d'une intégrale

Vladimir Arnold Trivium - conclusion

Einstein a écrit

Question de codimension en algèbre linéaire

Concevoir la notion d'application

Evaluation par QCM dans l'enseignement supérieur

Maths tordues ou tortues ?

Groupes et compagnie

Diamond signs et graffiti - de Donald Knuth à John Nash, passant par Jackson Pollock... (nouvelles photos ajoutées)

Archives

Blogs de maths

Autres sites

Blogs divers

Syndication