Maths et musique : quels concepts en commun ?
Dans ma vie musique et mathématiques tiennent une place à peu près égale. Les deux me passionnent, me procurent du plaisir, m’étonnent toujours et font que je reste un éternel élève. Quand je dis aux gens que je partage mon temps entre musique et maths, ça ne les surprend pas ; les mathématiques et la musique seraient liées, disent-ils. Mais en quoi consiste ce lien ? Généralement on me donnne trois types de réponses :
- La musique et les maths sont abstraites.
- Les deux utilisent des systèmes de notation illisibles pour le commun mortel.
- On y fait des calculs.
A mon avis tous ces points restent un peu à la superficie.
- Oui, les maths sont abstraites car elles sont construites sur un système d’axiomes qui n’est pas imposé par l’observation de la nature (comme les lois physiques) mais par un choix arbitraire soumis seulement à la logique ; et la musique est abstraite car elle ne dit rien de concret (comme une pièce de théâtre) et car on ne peut pas la toucher (comme une sculpture).
- Oui, les deux font recours à des systèmes d’écriture qu’il faut apprendre. Mais dans les deux cas la fixation par l’écrit n’est qu’un moyen et pas la finalité ; le théorème de Pythagore existe sans qu’un géomètre grec le trace dans le sable, et la musique existe pour être écoutée et non pour être lue. De plus, pas toutes les musiques sont écrites ; le solfège était inventé pour la musique classique européenne et ne se transpose pas forcément aux musiques d’autres cultures qui fonctionnent par transmission orale ou à la musique électronique de nos jours.
- Oui, dans les deux on peut être amené à faire des calculs. Mais encore les calculs ou la combinatoire ne constituent pas la finalité, ni dans la musique sérielle ou dodécaphonique, ni dans une triple-fugue de Bach, ni chez Bartók quand il place le climax d’un mouvement au moment qui correspond au nombre d’or.
Toutes ces réponses oublient un point essentiel qui, à mon avis, caractérise à la fois les sciences mathématiques et l’art de la musique :
La polyvalence des objets, ou le changement de référence
Une grande partie du travail d’un mathématicien consiste à considérer un même objet mais sous plusieurs angles différents, puis de traduire les observations d’un point de vue à l’autre. Ce qui est étonnant c’est qu’on peut en tirer, de ce pur travail de traduction, des conclusions intéressantes ! Et la même chose est vraie en musique ; une même mélodie, un même rythme, une même harmonie peuvent être ça ou ça
. Ca l’air assez flou, je vais m’expliquer sur des exemples simples.
Ca mais aussi ça — les maths comme la science des différents points de vue
Mon prof de physique avait l’habitude de se moquer des matheux qui, selon lui, ramènent tout énoncé à des affirmations triviales du genre 0 = 0. Il est vrai que les maths construisent un monde à partir de très peu. L’essentiel se fait en traduisant des différents points de vues. Proposons nous par exemple de prouver l’affirmation suivante.
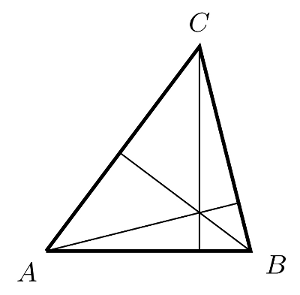
Proposition sur l’orthocentre. Les hauteurs d’un triangle sont concourantes, c’est-à-dire se coupent en un point commun.
 |
|
Les hauteurs se coupent en un point
|
Preuve. Soit ABC un triangle. Rappellons que, par définition, la hauteur issue de A est la droite passant par A et perpendiculaire à la droite (BC). Il ne faut pas la confondre avec la médiatrice sur [BC] qui, par définition, est perpendiculaire à [BC] et passe par le milieu de [BC].
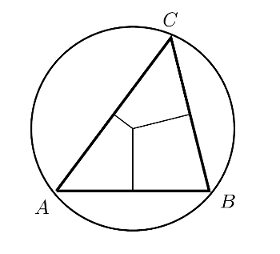
Il est facile de voir que les trois médiatrices du triangle sont concourantes. En effet, la médiatrice sur [AC] est l’ensemble des points équidistants à A et C ; et de manière analogue c’est vrai pour les deux autres médiatrices. Donc le point d’intersection des médiatrices sur [AC] et [BC] est équidistant à A et C et à B et C, donc il est aussi équidistant à A et B. Par conséquence il se trouve sur la médiatrice sur [AB].
En fait, l’intersection des trois médiatrices est le centre du cercle circonscrit au triangle.
 |
|
Les médiatrices se coupent
au centre du cercle circonscrit |
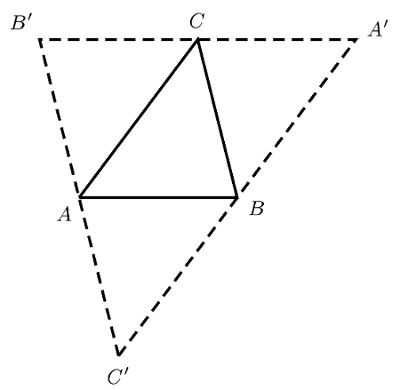
Maintenant revenons au problème de l’intersection des hauteurs. Nous construisons un nouveau triangle A’B’C’ comme indiqué dans le dessin suivant.
 |
|
Les hauteurs du petit triangle ABC sont
les médiatrices du grand triangle A’B’C’ |
Les droites (AB) et (CA’) sont parallèles ; de même (AC) et (BA’). Donc ABA’C est un parallélogramme, d’où l’égalité AB=CA’. De même on montre AB=B’C. Il en resulte que B’C=CA’ ou encore que C
est le milieu de [A’B’]. Par conséquence la hauteur issue de C dans le triangle ABC coïncide avec la médiatrice sur [A’B’] du triangle A’B’C’. On peut faire le même raisonnement sur les deux autres hauteurs.
Dire que les les hauteurs de ABC sont concourantes revient donc à dire que les médiatrices de A’B’C’ sont concourantes — et nous savons que cette dernière affirmation est vraie, q.e.d.
Résumé. Les trois hauteurs d’un triangle sont aussi les médiatrices d’un autre triangle. L’essentiel de la preuve consiste en la traduction d’un point de vue dans l’autre. L’objet mathématique, ici une droite, peut être est ça, mais aussi ça. C’est de la pure ambivalence, et le mathématicien en est le traducteur !
Un autre exemple est celui du problème des fourmis sur une tige qui semble compliqué au premier abord, mais est finalement trivial si on change de référentiel.
Ca mais aussi ça — la musique comme l’art de l’ambivalence
Un exemple basique concerne le rythme. Beaucoup de compositeurs (notamment Brahms) utilisent le fait que le nombre six est 3+3 mais aussi 2+2+2. Pour ceux qui connaissent le solfège (et le calcul des fractions), cela se traduit par l’égalité 6/8=3/4. Par conséquence on peut très bien faire la contrebande de quelques mesures 3/4 dans un morceau 6/8, sans gêner le groove général de la musique (au contraire ça en rajoute). Je crois que l’exemple le plus connu est la chanson I like to be in America de la West Side Story de Leonard Bernstein.
Un autre exemple vient de l’harmonie. Comme nous venons parler de triangles en maths, parlons de triades (accord de trois notes) en musique.
Prenons par exemple l’intervalle La-Do. Cette petite tierce peut faire partie de la triade La-Do-Mi (La-mineur) aussi bien que de la triade Fa-La-Do (Fa-majeur). C’est donc ça, mais aussi ça !
Une astuce des compositeurs est d’utiliser cette ambivalence au début d’une musique comme moyen de laisser l’auditeur dans le flou. Il ne sait pas si ça va aller vers mineur ou majeur ! Gustav Mahler le fait de manière géniale dans son fameux Adagietto (4e mouvement de la cinquième symphonie). En plus, il nous trompe encore à l’arrivée avec une appogiature, c’est-à-dire il nous fait entendre simultanément les deux tonalités La-mineur et Fa-majeur, seulement la harpe et le pizzicato de la basse confirment avec la fondamentale qu’on est bien dans Fa.
 |
|
Gustav Mahler : Adagietto de la 5ème symphonie
|
Pendant deux mesures l’auditeur craint d’être dans La-mineur, et quand il s’affirme finalement Fa-majeur, quelle satisfaction ! Vous pouvez l’écouter ci-dessous. Evidemment ce n’est qu’un exemple très basique et on en trouve beaucoup d’autres plus recherchés dans la littérature musicale (notamment les modulations ou l’enharmonie qui sont en analogie avec l’exemple des triangles cité en haut).
Ecouter cette musique ici.
Un dernier point commun entre maths et musique : c’est beau et ça ne sert à rien (enfin l’utilité n’est pas leur but premier). Mais une grande différence : les maths sont seulement belles pour ceux qui les font, tandis que la musique peut-être appréciée passivement.
D’ailleurs il y a des gens, plus formés que moi, qui réfléchissent aux liens structurels entre maths et musique et qui publient des recherches sérieuses sur ce sujet. De temps en temps je vais dans leur séminaire MaMuPhi à l’Ircam. Je me rappelle en particulier d’un exposé donné par le mathématicien et pianiste de jazz Guerino Mazzola ; il faisait le lien entre théorie des faisceaux et structure musicale. Je connais les faisceaux, je connais la musique, mais apparemment pas assez profondément pour avoir compris ces liens… Finalement, dans les deux domaines je ne suis qu’un working mathematician
ou working composer
qui ne se soucie pas trop des fondements souterrains 😉
Citation de Paul Erdös (1913-1996)
Why are numbers beautiful? It’s like asking why is Beethoven’s Ninth Symphony beautiful. If you don’t see why, someone can’t tell you. I know numbers are beautiful. If they aren’t beautiful, nothing is.

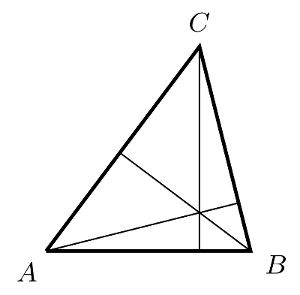


Cher alter ego, ce sont en effet quelques observations intéressantes que tu nous livres là. Il y a une grande différence entre mathématiques et musique que tu ne mentionnes pas : en mathématiques la devise est , c’est-à-dire on préfère les preuves courtes sans redondance et fioritures. Ce n’est pas vraiment le cas en musique où ce sont très souvent les détours et ornements inutiles qui font le style d’une composition.
Math et musique sont deux mouvements opposés: Math compactifie gestes en formules tandis que musique déploît formules en gestes. Ceci explique un peu mieux leur association/différence
Cher Guerino, entièrement d’accord. Je crois que c’est à peu près ce qui FilmTunes voulait dire (avec son langage un peu naïf de musicien).
Bonjour,
J’ai adoré vos exemples sur West Side Story et Malher. Perso, n’étant pas matheux, je m’intéresse toutefois à la Set Theory, je suis les travaux de l’Ircam et j’utilise notamment Open Music.
Une petite question, si vous avez le temps de vous y pencher. En effectuant une courte analyse – par curiosité – sur les 8 premières mesures du Quartet N° 4 de Beethoven avec la Set Theory, j’ai remarqué l’omni-présence de l’accord (ou triade) dit Viennois (seconde école)dit 3-5 {0, 1, 6}/{do, do#, fa#}, très utilisé notamment par Webern, je trouve ça très étonnant. Qu’en pensez-vous ?
http://www.deb8076.eu/AnalyseBee...
Merci pour votre commentaire et bravo pour vos observations. Mais je ne saurais pas répondre à votre question, car je n’ai pas le temps (ni l’envie) de me familiariser avec la Set Theory musicale. Vous devriez la poser à quelqu’un de l’Ircam ou encore à Guerino Mazzola.
Bizarrement, lorsque je fais de la musique je ne pense pas du tout en termes mathématiques. Toute la « musique combinatoire » à la Xenakis et Cie. m’est complètement étranger. Le résultat peut être intéressant mais, à mon avis, l’intéressant ne vient pas du côté combinatoire que, de toute manière, aucune oreille n’est capable de capter (seriez-vous capable de reconnaître la chanson Happy Birthday to You jouée à l’envers?). La devise du compositeur russe Rodion Chédrine me plaît quand il dit « peu importe les ingrédients, la chose principale est que la soupe soit bonne. » Donc si cette méthode de composition fonctionne, alors pourquoi pas? Mais elle n’est pas ma tasse de thé, et je n’aurai pas envie de l’utiliser lorsque je compose.
Je vous connaissais déjà du forum compositeur.org où j’interviens également une ou deux fois par an (mais pas en tant que MathOMan mais comme FilmTunes).
Le fait de dire qu’en maths le choix des axiomes est arbitraire, est pour le moins discutable. Qu’est-ce qui vous fait dire cela ?
Je ne suis pas platonicien mais je pense que les lois de la réalité s’imposent au mathématicien, comme au physicien,bien que ce ne soit pas de la même façon (car la "matière" du mathématicien est nettement plus noble).