Le transport de meubles vu par les matheux
Il est rare qu’une simple question de la vie quotidienne devient un problème de mathématiques quasiment insurmontable… mais ça peut arriver ! Il y a une quarantaine d’années le mathématicien autrichien Leo Moser se posait, probablement lors d’un déménagement entrepris tout seul, la question suivante :
Quelle est la taille maximale d’un canapé que je dois déménager horizontalement le long d’un couloir lorsque celui-ci présente un angle doit ?
Supposons que la largeur du couloir vaut 1. Comme un demi-disque de radius 1 passe clairement par l’angle, la taille l’aire maximale est minorée par \(\pi/2\approx1,5\7). Mais évidemment on peut faire mieux. L’anglais John Michael Hammersley proposa la solution ci-dessous en forme de combiné téléphonique, sans pourtant prouver que c’est la solution maximale (et effectivement Gerver a trouvé plus tard un sofa encore plus grand). En outre il démontre que la taille maximale est majorée par \(2\sqrt2\approx2,83\,.\)
On a donc un majorant et un minorant, mais quelle est la valeur exacte de la taille maximale ? Actuellement c’est toujours un problème ouvert. Pour monter des fonds de recherche pour bien attaquer ce problème important de mathématiques très appliquées, peut-être faudrait-il organiser une conférence inter-disciplinaire entre mathématiciens et la branche de scientifiques la plus concernée : les psycho-analystes !

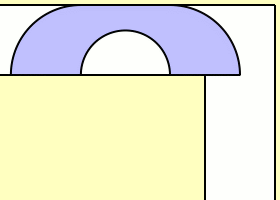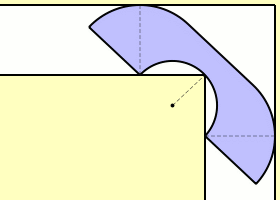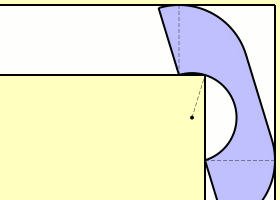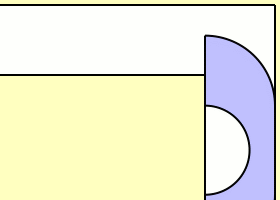
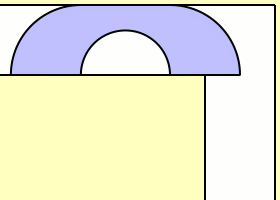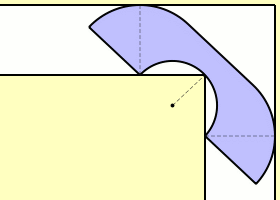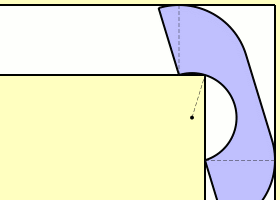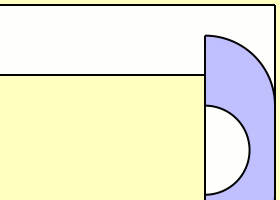



La taille c’est la longueur du plus grand segment inclus dans le canapé ?
Euh… j’ai tapé trop vite. Ca n’a pas l’air d’être ça si la taille d’un demi-disque de rayon 1 est pi/2. Donc la taille c’est l’aire ?
Oui, effectivement il s’agit de l’aire !
Bien entendu, interdit de basculer le canapé verticalement ou que sais-je d’autre, quoique ça pourrait faire un autre problème en 3D cette fois, potentiellement plus complexe quoi qu’on pourrait avoir des surprises. Et un canapé flexible ça compte ?
Ça me rappelle cette anecdote à propos d’Einstein (à moins que ce ne soit Schrödinger), qui aurait percé deux chattières dans sa porte : une pour son gros chat et une autre pour le petit…