Concevoir la notion d’application

Je me rappelle qu’au début de mes études de mathématiques, parfois une simple question de formalisme pouvait me poser des problèmes. Par exemple, j’avais du mal à jongler entre différents points de vue d’une notion a priori simple comme celle d’application. Voici quelques lignes qui pourraient sembler bêtes aux initiés, mais comme les livres expliquent rarement ce genre de choses en détail elles peuvent être utiles à ceux qui y sont confrontés pour la première fois — et notamment aux élèves et étudiants d’aujourd’hui qui, lors de leur parcours scolaire, ne rencontrent plus assez de théorie des ensembles.

Considérons une application (synonyme de fonction) d’un ensemble X dans un ensemble Y.

\(f\;:\; X \;\longrightarrow \;Y\,,\;\; x \; \longrightarrow\;f(x)\,. \)

(Désolé, la deuxième flèche devrait commencer par un pied mais mon plug-in LaTeX ne le permet pas.)

Si vous venez de passer le bac, vous avez déjà une notion intuitive de ce que c’est une application. Mais les mathématiciens possèdent plusieurs autres points de vue pour concevoir cet objet &#151 et chacun a sa raison d’être.

1. Point de vue y en fonction de x.
   C’est le point de vue habituellement enseigné au collège et au lycée. On conçoit x comme variable et y comme l’image qui change en fonction de x.
   Le schéma mental est le suivant.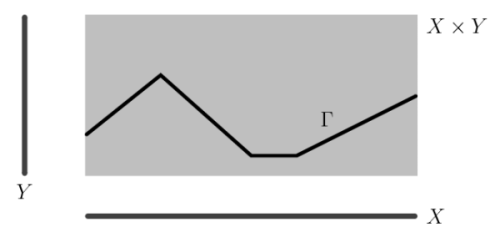

   

   L’ensemble de départ X est représenté horizontalement, l’ensemble d’arrivée Y est représenté verticalement.
   La donnée de l’application f revient à la donnée de son graphe \(\Gamma \subset X\times Y\) constitué des couples (x,f(x)), où x parcourt X.
   En disant x parcourt X, on adopte donc bien l’idée que la variable est x.
    

2. Point de vue collection d’éléments de Y.
   On peut aussi écrire l’application f en forme de famille \((f(x))_{x\in X}\). On oublie donc de spécifier l’ensemble d’arrivée Y.
   En général, une famille \((y_j)_{j\in J}\) dans Y n’est rien d’autre qu’une application

   \(y\;:\; J \;\longrightarrow \;Y\,,\;\; j \; \longrightarrow\;y_j\,, \)

    
   où l’ensemble de départ J est appellé l’ensemble d’indices ; très souvent il n’a pas d’importance et peut être remplacé par un autre ensemble de même cardinal. Ce qui compte dans ce point de vue c’est simplement la collection des images de l’application.
   Dans certaines situations un bon choix de l’ensemble d’indices peut raccourcir les écritures. Par exemple, si \((b_j)_{j\in J}\) est une base d’un K-espace vectoriel E, alors tout vecteur v de E se décompose comme combinaison linéaire

   \(v=\sum_{j\in J} \lambda_j\, b_j\:,\)

   où \((\lambda_j)_{j\in J}\) est une famille de scalaires presque tous nuls (c’est-à-dire l’application \(\lambda\;:\; J \;\longrightarrow \;K\,\) est nulle sauf en un nombre fini de points ; cela est nécessaire pour pouvoir prendre la somme). Mais si on conçoit la base non comme une famille de vecteurs mais comme un sous-ensemble B de l’espace E, alors on peut la prendre elle-même comme ensemble d’indices et écrire simplement

   \(v=\sum_{b\in B} \lambda_b\, b\:.\)

    

3. Point de vue les fibres en fonction de y.
   Pour chaque y dans Y on appelle fibre de f en y (ou ensemble de niveau y) l’ensemble de tous les antécédents de y, noté
   
    
   \(f_y\;=\;f^{-1}(\{y\:\})\:=\:\{\:x\in X\; :\; f(x)=y\:\} \,.\)

    
   Connaître une application revient à connaître la collection de ses fibres. C’est donc y qu’on considére comme variable. On s’aide du schéma mental suivant.
    

   

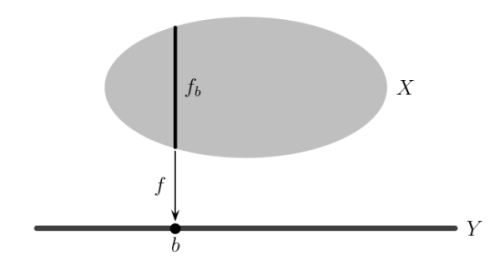
   L’espace de départ est projeté sur l’espace d’arrivée.
   L’application est injective (resp. surjective resp. bijective) si et seulement si chaque fibre possède au plus (resp. au moins resp. précisément) un élément.
   
    

Une conséquence naturelle du point de vue des fibres est la factorisation canonique, que nous allons expliquer ci-dessus et dont la quintessence se résume ainsi :

L’ensemble des fibres non-vides d’une application est une partition de l’ensemble de départ et a le même cardinal que l’image de l’application.

Factorisation canonique

Nous nous proposons de montrer que toute application est la composée d’une surjection, d’une bijection et d’une injection. Soit donc f une application de X vers Y.
On considère son image

\(\tilde{Y} = f(X)\:\subset\:Y\)

et l’espace des fibres

\(\tilde{X} = \{\,f^{-1}(\{y\})\:|\: y\in \tilde{Y}\,\}\:\subset\:{\scr P}(X).\)

Ainsi l’espace des fibres est le quotient de X par la relation d’équivalence  ~  qui est définie par  x ~ x’  si et seulement si f(x) = f(x’). Il est clair que \(\tilde{X}\) et \(\tilde{Y}\) sont en bijection. Plus précisément il existe une surjection \(\pi\), une bijection \(\tilde{f}\) et une injection \(j\) tel que le diagramme suivant commute.

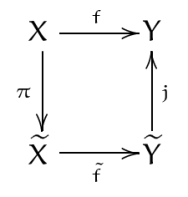
En effet, il suffit de prendre pour \(\pi\) la projection canonique sur le quotient X/~, c’est-à-dire l’application qui à chaque x dans X associe la fibre de f en f(x) ; puis pour j l’injection naturelle, et enfin pour \(\tilde{f}\) l’application qui envoie une fibre sur l’unique élément dans Y qui est son image par f. Il est alors évident que f est la composée

\(f= j\circ \tilde{f}\circ \pi\).

Un avant-goût de la suite

Concevoir une application comme la collection de ses fibres est très fréquent en topologie, géométrie algébriques et théorie des singularités. On fait varier un point dans l’espace d’arrivée pour observer, dans l’espace de départ, la manière dont varie la fibre au-dessus de ce point. Un exemple très basique est l’application

\(f\;:\; \mathbb{R}^3 \;\longrightarrow \;\mathbb{R}\,,\;\; (x,y,z) \; \longrightarrow\;ax+by+cz\,, \)

 
où a,b,c sont des réels fixés non tous nuls.
La collection des fibres est constituée de plans parallèles. Il s’agit donc d’un feuilletage de l’espace \(\mathbb{R}^3\) par plans (comme un feuilleté). Les fibres se ressemblent toutes ; on a même ce qu’on appelle une fibration globalement triviale.

Plus généralement, si f est une fonction différentiable et si on fait varier le point dans l’espace d’arrivée sans toucher les valeurs critiques, alors localement les fibres se ressemblent toutes (fibration localement triviale).
En revanche, si on passe par une valeur critique alors la nature des fibres peut changer. Par exemple si on traverse la valeur critique 0 de l’application

\(g\;:\; \mathbb{R}^2 \;\longrightarrow \;\mathbb{R}\,,\;\; (x,y) \; \longrightarrow\;x^2+y^2\,,\)

dans le sens décroissant, alors la fibre est d’abord un cercle, puis dégénère en un point et, enfin, devient vide — une catastrophe a lieu au sens de la théorie des catastrophes de René Thom.

Tout ça devient plus intéressant dans le complexe. Les fibres de

\(g\;:\; \mathbb{C}^2 \;\longrightarrow \;\mathbb{C}\,,\;\; (x,y) \; \longrightarrow\;x^2+y^2\,,\)

sont des surfaces réelles (courbes complexes ou surfaces de Riemann). Et au lieu de traverser la valeur critique 0, on peut la contourner avec un petit lacet dans le plan complexe et observer la déformation de cette surface le long du lacet. Evidemment à la fin on retrouve la même surface qu’au début du lacet, mais lors du trajet certaines caractéristiques se sont déplacés continûment et ont échangés leurs places… (monodromie).